Def 3.1.
n개의 서로 다른 요소로부터 만들 수 있는 모든 순서화된 목록의 수는 n*(n-1)*(n-2)*...*1 로 계산이 가능하다.
이를 n! 이라고 하자. (Factorial)
단 0!=1 이다.
증명)
1...n 개의 숫자열이 있다고 할 때,
1을 배치할 때는 n 개의 경우의 수
2를 배치할 때는 n-1 개의 경우의 수
3을 배치할 때는 n-2 개의 경우의 수...
n을 배치할 때는 n-n+1 개의 경우의 수가 있다.
=> n*(n-1)*(n-2)*...*(1)
Def 3.2.
A : n 개의 element set, K는 0~n까지로 정의된 정수 sample space의 element 일 시,
( A: n-element set, K ∈ [n] )
A의 k 순열은 A의 크기가 k인 부분집합의 순서화된 리스트이다.
간단히 말해, k-순열은 집합 A에서 임의의 k개 원소를 선택하고, 그 선택된 요소들로 만들 수 있는 모든 가능한 순서의 나열이다. k 순열의 총 개수는 n!/(n-k)! 로 계산된다.
증명)
A에서 k개의 원소를 뽑아 나열하면,
n(n-1)(n-2)...(n-k+1)의 경우의 수로 나열 가능 (접은글 참고)
=> n(n-1)(n-2)...(n-k+1) = n!/(n-k)!
* approx. of n!
=> ai,bi가 순열일 때, ai bi가 asymptotically equal이라는 것은 n이 무한대로 갈 때, lim(i->∞) ai/bi = 1이라는 뜻이다.
ex ) an = n + sqrt(n), bn = n. -> lim(n->∞) (1+1/sqrt(n)) = 1
* 스털링 근사식 : n! ~= (n^2)*(e^-n)*sqrt(2*PI*n) 이다.
=> 이는 매우 큰 n에 대해 n!의 값을 계산할 때 유용하다.
ex) Derangement (hat check prob)
정의 : 어떤 순열 p에서, element x가 fixed point인 경우는 f(x) = x임을 의미한다.
즉, fixed point는 순열 쌍에서 원래 있던 자리에 그대로 위치하게 된 원소를 의미한다.
Pk(n) = 집합 {1,2,...n}의 순열 중 정확히 k개의 fixed point를 가진 순열이 나올 확률이라고 정의하자.
따라서 P0(n)은 고정점이 하나도 없는 Derangement 순열이 나올 확률이다.
D(n)은 n개의 원소에서 Derangement 순열의 갯수라고 정의하자.
Q: P0(n) ?
A :
i ) n이 1일때,
D(1) = 0 개
- 하나의 원소만 존재하므로 자리가 변할 수 없다.
ii ) n이 2일 때,
D(2) = 1 개
- (1,2),(2,1). 따라서 1/2
iii ) n>2
t = 생성된 derangement에서 첫번째 위치의 정수라고 가정.
case 1. 1이 t 포지션에 있을 때. (t와 1의 위치가 교환된 case)
(1...t...)->(t...1....) => 2개 원소의 위치가 결정되었으므로, 남은 원소는 n-2가지이다. 따라서, (n-1)*D(n-2)
case 2. 1이 t 포지션에 없을 때.(t와 무언가가 교환된 case)
(1...t...)->(t...?...) => t의 자리가 결정. (n-1)*D(n-1)
따라서 D(n)은 다음과 같이 재귀적으로 정의될 수 있다.
D(n) = (n-1)D(n-2) + (n-1)D(n-1)
=> P0(n) = 1/2! -1/3! + 1/4! - 1/5! +...(-1)^n/n! ~= e^-1 ~= 0.368 => 불일치 순열이 일어날 확률
(포함 배제 원리 이용) - 포함 배제 원리는 다음 포스팅에 추가 설명하겠음.
3.2. Combinations
Def ) n 크기 set에서 j개의 원소를 가진 고유한 부분 집합의 수는 n(C)j 로 나타낼 수 있다.
예를들어, U = {a,b,c}에서 3(C)0 = 1 = { ∅ }, 3(C)1 = 3 = {a},{b},{c}, 3(C)1=3={a,b},{b,c},{a,c}이다.
여기서, Permutation과 다른 점은 n개의 원소를 "나열"한다는 개념의 Permutation과 달리,
Combination은 "고유한" 부분 집합의 수만 따지므로, order의 개념이 없다.
즉, Combination에서 {a,b} = {b,a} 인 것이다.
* 파스칼의 정리
0<j<n의 n,j 정수에 대해, n(C)j = n-1(C)j + n-1(C)j-1
증명)
size n의 집합에서 임의의 원소 A를 선택했을 때
i) A가 j의 원소였을 경우 : 나머지 n-1 중 j-1개를 고르면 된다. => n-1(C)j-1
ii) 아닐 경우 : 나머지 n-1 중 j개를 고르면 된다. n-1(C)j
=> n(C)j = n-1(C)j-1 + n-1(C)j
(파스칼의 삼각형)
Thm ) n(C)j = n! / j! * (n-j)! (j-순열의 갯수에서 j!을 나눈 형태)
증명
nPj = size n의 set에서 j 개의 원소를 지닌 ordered list의 수 = j 순열
nPj = n(C)j * j! (ordered list이므로, 조합에서 순서 개념을 더해준다. 즉, n개 중 j개의 원소를 뽑고, 이들을 나열하는 경우의 수 j!을 곱해주는 것이다.)
따라서, n(C)j = nPj / j! = n! / j!(n-j)!
문제.
ex ) 13개의 값을 4개의 종류로 지닌 카드를 뽑을 때, 5장 중 4개의 값이 전부 같을 확률은
4개가 13개의 값 중 하나로 같을 경우는 13개 * 나머지 1장 남은거 뽑기 48
=> 13*48
-> 총 카드 5장 뽑을 확률은 52(C)5. 따라서 13*48/(52(C)5) = 0.0024
ex) 3장의 값이 같고 나머지 2장의 값이 같을 확률은
13 * (같은 value를 지닌 4개의 종류 카드 중 3장 뽑을 확률) + 12 * (같은 val.을 지닌 4개의 종류중 2장 뽑을 확률)
=> (13*4(C)3 + 12*4(C)2) / (52(C)5)
* Bernoulli trial
=> Bernoulli tiral은 단 두가지 결과(True or False)를 지닌 독립 확률 실험이다. (ex: 동전 던지기)
=> 따라서 T, F가 (p) (1-p) 의 확률로 구성된다. 보통 p,q로 표현하며 자연스럽게 q=1-p가 된다.
* Binomial Probabilited
=> n번의 베르누이 시행에서 정확히 k번 성공할 확률을 계산하는 것으로, 기호 b(n,p,j)로 나타낸다.
(n번의 시행중 p의 확률로 j번 성공할 확률)
ex) q=1-p
b(3,p,0) => q^3
b(3,p,1) => 3(C)1*p*q^2 (3번 중 1번이 성공할 것임)
b(3,p,2) => 3(C)2*p^2*q (3번 중 2번이 성공할 것임)
b(3,p,3) => p^3
* Binomial Distribution
Def 3.6)
n : positive integer, 0<=p<=1, n = 베르누이 시행에서 성공의 횟수
다음을 이항 분포라고 부른다. => b(n,p,k) = n(C)k * p^k * q^(n-k)
(n번의 시도 중 k번의 성공한 횟수를 뽑고, k번 성공확률 * 나머지 실패할 확률)
* Binomial Expansion
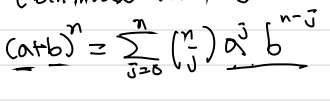
이항 정리 증명
(a+b)^n = (a+b)*(a+b)*...*(a+b) => 이 n개의 (a+b) 들은 a^j*b^(n-j) 들로 구성되고, 이게 몇 개있냐에 따라 계수가 결정됨.(n(C)j)
Special Case)
만약 a=b=1 일 시, 2^n
a=1, b=-1 일시 0
* 포함 배제 증명에 들어가서 더 자세히 표현하면 a = 1, b = -1의 식 표현은다음과 같다.

* Inclusion-Exclusion Principle
set of event A의 set {A1,A2...,An}
=> 이 set의 총합은 확률의 총합 - 이 확률들의 교집합들의 합+여러번 빠진 확률의 합이다.
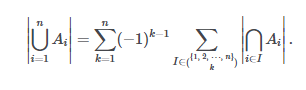
증명
임의의 원소 x가 모든 A set에 포함되는 outcome이라고 해보자.
이 원소는 위에 제시된 포함 배제 식의 좌변 합집합 크기를 딱 1만큼 늘릴 것이다. (전부에 포함되기 때문에)
그러면 우변에도 x가 1만큼만 보태주면 되는 문제인 것이다.
A들 중 x를 원소로 갖는 것들의 수를 k라고 하자. (A0~Ak).
이 때, 우변을 보면 k개 집합의 교집합에 (-1)^k-1를 곱하여 더해주므로 이 x가 우변에 더해줄 크기는
k(C)1 - k(C)2 +k(C)3 +...+ (-1)^(j-1)*k(C)k일 것이다.

그런데 이항 정리에서 a=1, b=-1일 때 위의 사진과 같이 식이 정리되며, 이 값은 0이다.
이를 전개해보면 다음과 같이 전개될 것이다.
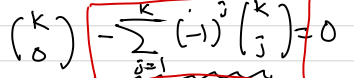
여기서 k(C)0은 1이므로, 나머지 부분의 값이 1이 되어야 된단 것을 알 수 있다.
그런데 나머지 부분의 값은 k(C)1 - k(C)2 +k(C)3 +...+ (-1)^(j-1)*k(C)k 의 표현과 동등하다.
따라서 x가 보태어주는 크기는 1이다.
ex) derangement
A={a1,...an}에서
Ai : ai가 fixed point일 경우 라고 가정
P(Ai) = n개의 포인트 중 한자리를 ai가 가져감. = (n-1)! / n! = 1/n
=> P(A1 U A2 U A3... U An)을 구해서 1에서 빼면 derangement 확률이 나올 것이다.
i) 각 자리가 개별로 고정점일 경우의 확률 합.

= 1/n * n = 1
(사실 이렇게 생각 안해도 모든 점이 기존의 자리를 유지하는 경우의 수는 한개이다.)
ii) 2개의 자리가 고정점일 경우의 확률 합

= 2개가 고정점일 확률 * 고정점 2개를 고를 확률
= (n-2)!/n! * n(C)2 = 1/n(n-1) * n(n-1)/2! = 1/2!
iii) 그 이상
=> 같은식으로 정리되어 (n-k!)/n! * n(C)k = 1/k!이다.
이 때, 포함 배제 원리에 의해
1 - 1/2! + 1/3! + ... = P(A1 U A2 U A3 U...U Ak)
따라서 1 - P(A1 U A2 U A3 U...U Ak) = 1/2! - 1/3! + 1/4! +.... ~= e^-1
'개인 공부' 카테고리의 다른 글
| 데이터 과학 - 기상청 최고 기온, 최저 기온 데이터 크롤링하기 (0) | 2024.04.01 |
|---|---|
| 확률 및 통계 - 4. Conditional Probability (0) | 2024.03.31 |
| 확률 및 통계 - 2. Continuous Proability Densities (0) | 2024.03.12 |
| 확률 및 통계 - 1. Discrete Proability Distributions (3) | 2024.03.07 |
| NS-3 독학 - 完. Seventh.cc (0) | 2024.01.15 |