* Discrete Conditional Probability
- 어떤 Sample Space 상에서 Event E가 이미 일어난 뒤라고 가정해보자. 그렇다면 해당 사실이 다른 Event F에 영향을 미칠까? 미친다면 얼마나 미칠까. 이를 계산해보자.
Def)
P(F|E) = E가 일어난 공간에서의 F가 일어날 확률.
Ex)
주사위를 굴리자.
Experiment : 주사위를 굴림
X : r.v(out come)
E : event {E | X>4}
F : event {E | X=6}
=> P(F|E)는 이미 E가 일어난 시점을 가정하므로 Sample space가 { 5, 6 } 으로 정의된다.
이 Sample Space에서 P(F)는 1/2이다.
따라서 P(F|E) = 1/2
* 위의 구하는 과정을 따라가보면 event E와 F가 관계가 없는 사건일 시 당연히 확률에 변화가 없을 것임을 알 수 있다.
(독립 사건)
Sample space S = {w1,w2...,wr}, S에 대한 분포함수 m(x)가 있다고 가정하자.
이 때, m(wi | E)는 다음과 같이 정의될 수 있다.
1. wi가 E의 element가 아닐 때
m(wi | E) = 0
2. wi가 E의 Element일 때
m(wi | E) = c * m(wi)
! c는 constant이며, E가 일어남으로 인해 영향을 준 정도이다.
이제 i = 1~r 까지 모든 m(wi | E)를 더해보자.
Σ m(wi | E) = 1 = c * Σ m(wi)
그런데 Σ m(wi) = P(E) 이다.
따라서 c = 1/P(E)가 되어야하며, m(wi | E) = m(wi) / P(E)임을 알 수 있다.
general event F 에 대해, P(F|E) = m(wi) / P(E) 이고 이때 이 wi들은 F와 E에 공유되는 원소들일 것이므로
m(wi) / P(E) = P(F n E) / P(E)로 정의 가능하다.
* 결론 : P(F | E) = P(F n E) / P(E)
Ex)
위의 접은글 Ex)의 경우를 해당 식으로 구해보면
P(F n E) / P(E) = P(F) / P(E) = (1/6) / (1/3) = 1/2
(* F ⊂ E)
Ex)
2개의 박스가 있고, Box I 에는 2개의 검은색, 3개의 흰색 공이 들어있다.
Box II에는 1개의 검은색, 1개의 흰색 공이 들어있다.
이 때 검은색 공을 뽑았더니 Box I의 공이었을 확률을 구하시오.
=>
I : Box I의 공을 뽑을 확률
II : Box II의 공을 뽑을 확률
B : Black color를 뽑을 확률
P(I | B) = P(I n B) / P(B)
P(B) = P(B n I) + P(II n B) = 1/2 * 2/5 + 1/2 * 1/2 = 9 / 20
P(I n B) = 1/2 * 2/5 = 1/5.
그러므로, (1/5) / (9/20) = 4/9
Def)
특정 사건 E가 일어난 뒤 사건 F의 확률에 어떠한 영향도 미치지 않을 시, "Independent events"라고 부른다.
이 때, P(E | F) = P(E)이다.
* 독립조건 : P(E n F) = P(E)P(F)
증명)
사건 E와 F가 연관이 없을 시, P(E | F) = P(E)라는 정의에 의하면,
P(E | F) = P(E n F) / P(F) = P(E)이다. 따라서, P(E n F)= P(E)P(F)가 되어야 한다.
EX)
동전을 두번 던져 앞면이 나올 확률 p, 뒷면이 나올 확률 q의 베르누이 시행을 한다고 하자.
이 때, 각 시도는 서로 독립임을 증명하라.
i) P({H, H}) = p^2
ii) P({H, T}) = p*q = pq
= E : 1st toss에 head, F: 2nd toss에 tail
=> P(E) = p^2 + pq = p(p+q) = p
=> P(F) = q^2 + pq = q(p+q) = q
=> P(E n F) = pq = P(E)P(F)
따라서 event E와 F는 Independent events 이다.
EX)
동일한 시험에서
I : 1st toss에서 head
J : head가 2번 나올 확률일 시, 이들의 독립여부를 판단하라.
P(I) = 1/2
P(J) = 1/4
P(I n J) = 1/4 =/= P(I)P(J)
따라서 독립 관계가 아니다.
Def)
A set of events A={ A1,A2...,An}이 P(A1 n A2 n A3 n A4 n ... n An) = P(A1)P(A2)...P(An)일 시, 이들을 mutally independent라고 한다.
=> 따라서 A와 B가 독립일 시, A와 B의 여집합 Bc도 독립이다.
증명)
P(A n B) = P(A)P(B)
P(Bc) = 1 - P(B)
* P(A n Bc) = P(A)P(Bc)임을 증명.
P(A n Bc) = P(A)P(Bc) = P(A)(1-P(B)) = P(A) - P(A)P(B) = P(A)-P(AnB)
=> P(A n Bc) = P(A)-P(AnB)
=> P(A n Bc) + P(AnB) = P(A).
따라서 명제는 참이다.
* Joint distribution functions and independence of Random Variables(결합 분포)
만약 동전 2개를 3번 던진다고 생각해보자.
가능한 결과는 8개가 될 것이다.
X : 8개의 가능한 결과에 대한 random val.
Xi : i번째 outcome에 대한 random val.
m : Xi의 Distribution function
(즉, r.v X1,X2,X3이 존재하며 X : {X1,X2,X3} 의 형태를 취한다.)
이 때, X의 sample space는 각 Sample Space를 곱한 것이다.
(S1 * S2 * S3)
Def)
X1 ... Xn : n개의 r.v.
Ωi : Xi의 sample space
라고 할 시, joint r.v. X={X1,X2,...,Xn}은 순서가 적용된 결과의 순서쌍으로 표현된다.
이 때, X의 sample space는 Ω1* Ω2*...* Ωn이 된다.
그리고 이에 대한 distribution function은 joint distribution function이라고 부른다.
ex)
앞서 말한 Coin toss에서 이어서 생각해보자.
X = {X1,X2,X3}이며,
P(X = {a1,a2,a3} = P(X1=a1)*P(X2=a2)*P(X3=a3)일 것이다. (X1,X2,X3는 서로 독립)
Yi를 i번 던졌을 때 head가 등장한 횟수라고 해보자.Y = {Y1,Y2,Y3}Y의 sample space ={{a1,a2,a3} 0=<a1<=1, 0<=a2<=2, 0<=a3<=3}
P(Y={1,0,1}) = 0 * 애초에 1번째에서 head가 나왔는데 2번째에서 head의 갯수가 0인 것은 정의되지 않는다.P(Y1 = 1) = 1/2P(Y2 = 0) = 1/4P(Y3 = 1) = 3(C)1/8P(Y={1,0,1}) =/= P(Y1=1)P(Y2=0)P(Y3=1) - 독립이 아님
Def)
joint r.v.들은 만약 P(x1=r1,x2=r2,..,xn=rn) = P(x1=r1)P(x2=r2)...P(xn=rn)을 만족 시, mutally independent다.
그러므로 X에 대한 joint distribution function은 mutally independent가 보장된다면 개별 r.v.의 distribution fuction m의 곱으로 표현이 가능하다.
EX)
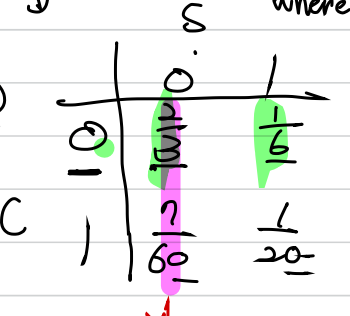
P(s,c)가 다음과 같은 분포를 가질 때, C에 대한 marginal distribution은?
=>
mc: marginal distribution function of C
mc(c) = 모든 s에 대한 mc(c)의 합.
mc(0) = m(0,0) + m(0,1) = 2/3 + 1/6 = 4/6
mc(1) = m(1,0) + m(1,1) = 7/60 + 3/60 = 10/60 = 1/6
똑같이 ms도 구해보면
ms(0) = m(0,0) + m(1,0) = 2/3+7/60 = 47/60
ms(1) = m(0,1) + m(1,1) = 1/6+1/20 = 10/60 + 3/60 = 13/60
P(1,1) = 1/20
mc(1)*ms(1) = 13/360
P(1,1) =/= mc(1)*ms(1) 따라서 독립이 아니다.
* Independent Trials Processes
Def)
r.v. {X1,X2,...,Xn}들이 같은 distribution을 지니며 서로 mutally independent라면(i.i.d) 이들은 independent trials이다.
=> 개별 r.v.에 대해 Sample Space R={r1,...rs}를 가진다 하자. 그리고 이들의 개별 distribution function은 mx, joint distribution function은 m이라고 하자.
이때 sample space는 R^n으로 정의되고,서로 mutally independent이므로 m(w) = mx(w1)*mx(w2)...*mx(wn)이다.
Ex)
p의 성공확률을 지니는 Bernoulli trial에 관해 Xj=1이면 j-th outcome이 성공인 것으로 정의하자.
Sn = X1+X2+...+Xn을 정의하라.
=>
베르누이 시행이므로 각 r.v.들은 mutally independent이고, b(n,p,q)의 같은 distribution을 가진다. (i.i.d)
따라서 P(Sn=j) = n(C)j * p^j * q^(n-j) 이다.
* Bayes' Formula
Set of events H1,..,Hm이 mutally disjoint이며,
Ω : H1 U H2 U...U Hm 이고, P(H1)...P(Hm) 들이 알려져있고,
E(event)에 대한 P(E|H1), P(E|H2),..,P(E|Hm) 또한 알려져있다고 가정하자.
이 때, P(Hi | E) = P(Hi n E)/P(E) = P(Hi)*P(E|Hi) / (P(H1 n E)+P(H2 n E) ..+P(Hn n E)) = P(Hi)P(E|Hi) / ΣP(Hk)*P(E|Hk)

즉, P(Hi)P(E|Hi) / (사건 E의 전확률)이 되는 것이다.
Ex)
P(M1) = 0.2
P(M2) = 0.3
P(M3) = 0.5
P(A|M1) = 0.01
p(A|M2) = 0.02
P(A|M3) = 0.03
P(M2|A)?
=>
P(M2|A) = P(M2 n A) / P(A) = P(A|M2)*P(M2) / (P(A n M1) + P(A n M2) + P(A n M3))
분자
0.02*0.3= 0.006
분모
P(A|M1)P(M1) + P(A|M2)P(M2) + P(A|M3)P(M3) = 0.01/*0.2 + 0.02*0.3 + 0.03*0.5 = 0.002 + 0.006 + 0.015
따라서 0.006 / 0.023 = 0.26
* Continouous Conditional Probability
X : conti. r.v. with density function f(x)
E : event with P(E)>0
일 시, f(x|E) = f(x)/P(E) (if x ∈ E), 0 (else) 로 density function의 정의가 가능하다.
또한 모든 사건 F에 대해
f(x)/P(E)를 E n F의 구간 만큼 적분한 값이 P(F|E)가 된다.
Ex)
[0,1]의 임의의 점에 대해
f(x) = 1 (0<=x<=1), 0 (otherwise)
* 이 상황에서 우리는 point가 [0,1/2]안에 있다고 가정하자.
point가 [1/6, 1/3]에 있을 확률은?
=>
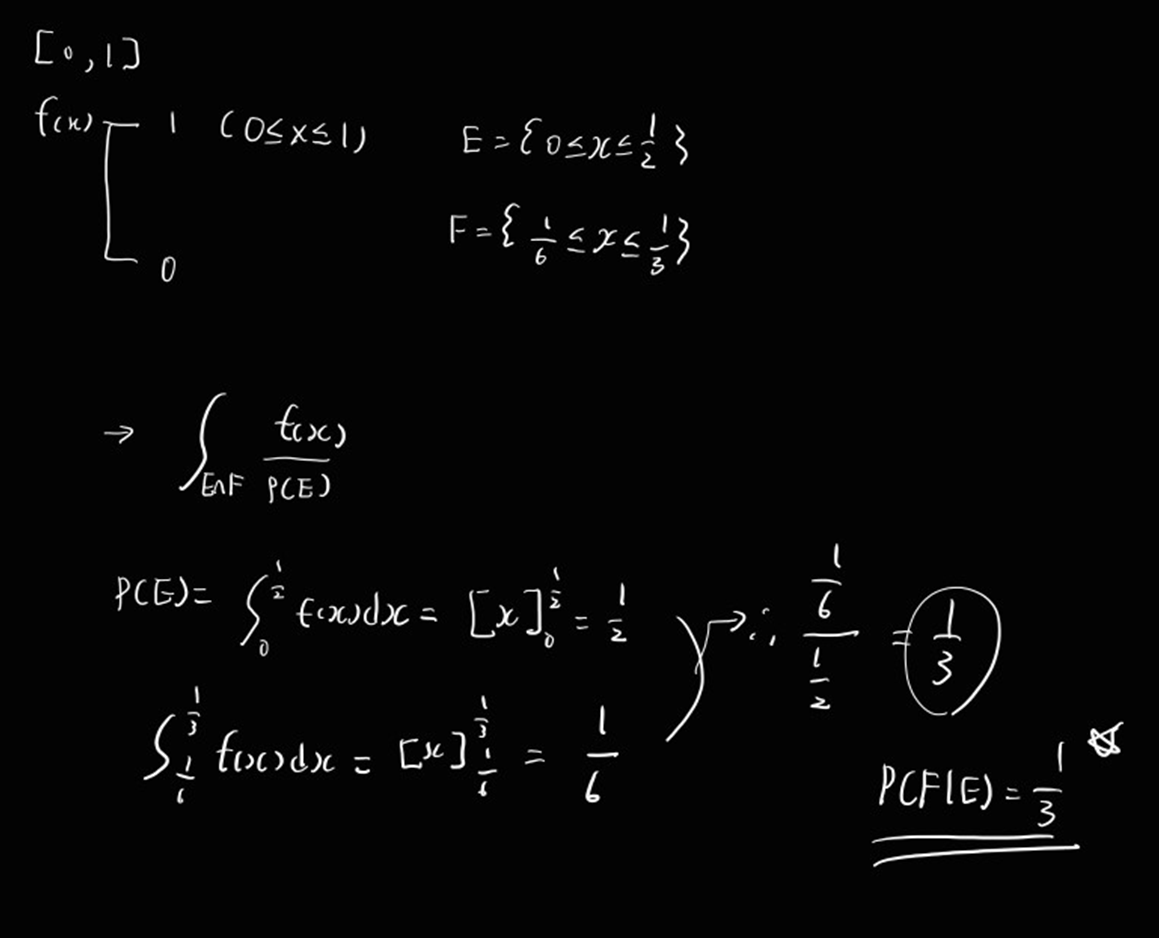
Hard Ex)
E = {(x,y) : y>=0}
F = {(x,y) : x^2 + y^2 <= 1/4}
f(x,y) = 1/PI (if x^2+y^2=1), 0 (otherwise)
P(F|E)?
=>

'개인 공부' 카테고리의 다른 글
| 데이터 과학 - 1. Introduction to Data Science (0) | 2024.04.02 |
|---|---|
| 데이터 과학 - 기상청 최고 기온, 최저 기온 데이터 크롤링하기 (0) | 2024.04.01 |
| 확률 및 통계 - 3. Permutations & Combinations (0) | 2024.03.27 |
| 확률 및 통계 - 2. Continuous Proability Densities (0) | 2024.03.12 |
| 확률 및 통계 - 1. Discrete Proability Distributions (3) | 2024.03.07 |