이전 복습 문제)

사건 E와 F가 서로 독립임을 증명하기.
* Joint density & cumulative distribution function
Def.
X1~Xn이 Conti. Random Variable이고, X'가 (X1...Xn)의 Joint Variable일 경우,
X'의 Joint cumulative distribution func.는 F(x1,...xn) = P(X1<=x1, X2<=x2,...,Xn<=xn) 이고 이들은 각 변수에 대해 모두 적분해주어 구할 수 있다.

또한 만약에 F(x)가 n차 미분이 가능하다면, 다음을 통해 다시 Joint density func.를 구할 수 있다.

ex)

* Independent Random Variables
Def.
X1 ... Xn 들이 Conti. r.v. 이고 이들의 c.d.f. F1(x), F2(x),...,Fn(x)가 정의되어 있다고 하자.
이 때, f(x1,...,xn) = f(x1)*f(x2)*...*fn(xn)일 시, 이들을 mutually independent라고 한다.
Ex)
unit square에서 point를 하나 고른다고 해보자.
이 때, 정해진 두 점은 w1,w2이고, 해당 점의 ditribution function은
f(w1,w2) = 1 (0<=w1,w2<=1), 0 (otherwise)이다.
이 때 3개의 r.v. X1,X2,X3는 다음과 같이 정의된다고 하자.
X1 = w1^2, X2=w2^2, X3=w1+w2.
(이 때, F1(X1), F2(X2), F3(X3)는 문제로부터 제시된다.)
Q1. X1과 X2는 independent 인가?

Q2. X2와 X3는 independent 인가?

ex) joint density function f(x,y) of X,Y
f(x,y) = kx^2y^2 (x^2+y^2<=1), 0 (otherwise) - 단 k=/=0.
Q) X,Y are independent?

* Independent trials
Def.
i.i.d의 r.v.들의 나열을 Idependent trial이라고 부른다.
* Important Distributions and Densitied
* Discrete Uniform Distribution
X : size n의 sample space S에서 추출된 r.v.
=> X가 균일 분포를 따른다는 것은 S에 속한 모든 원소 u에 대해 equally likely 1/n을 가진다는 의미이다.
* Binomial distribution
X1,..Xn : Bernoulli trials with success prob. p
Xi = 1(p), 0(q)
일 때, X = X1+X2+...+Xn (# of Sucess)
그러면 다음과 같이 정의된다.

* Geometric Distribution
- Bernoulli trial을 무한히 시도한다고 가정하자. (0<p<1)
r.v. T : 첫번째 성공이 나올 때까지 시도한 횟수
=> P(T=1) = p, P(T=2) = pq, P(T=3)=pq^2...,P(T=n)=q^(n-1)*p (T는 discrete distribution을 가진다.)
이 떄, P(T=j+1)/p(T=j) = q 이며, q<1이다.
좀 더 일반화하여, T가 다음과 같은 분포를 가지면 Geometric distribution이라고 한다.
P(T=j) = q^(j-1)*p = m(j)
=> X가 geometric distribution을 가지고 Y가 해당 조건을 만족하는 최소의 정수라고 하자.
(1-q^Y >= rnd, rnd=[0,1]사이 random number)
P(Y=j) = P(1-q^j >= rnd > 1-q^(j-1))
= (1-q^j)-(1-q^(j-1))
= q^(j-1)-q^j = q^(j-1) * (1-q) = q^(j-1)*p
따라서 Y 역시 geometically distribution을 가진다.

Ex)
1 or 0 customer comes for each time unit.

* Negative Binomial Distribution
ex) coin toss with prob. p of head comes up, k>0, toss until k-th head appears.
r.v. X = # of tosses.
i) k=1 : X는 geometric distribution을 가진다.
ii) 일반적인 k에 대해 X는 negative binomial distribution을 가진다고 한다.
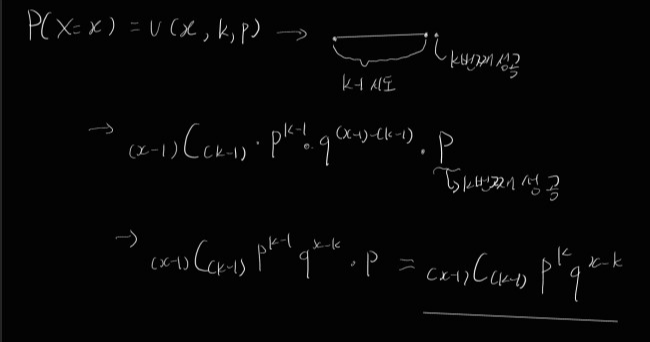
즉, 음이항분포(Negative Binomial Distribution)은 연속된 Bernoulli trials에서 발생하는 성공 횟수를 새는데, 이 때 특정한 수의 실패가 발생하기 전까지 계속, 혹은 특정한 성공 횟수가 발생할 때까지 계속하는 것이다.
기존의 이항분포는 시행 횟수가 고정되어있을 때(n) 성공 횟수를 모델링하는 반면, 음이항 분포는 목표 횟수(k)가 고정되고, 이 때 성공 횟수를 모델링하는 것이다.
* Poisson distribution
특정 시간 동안 또는 특정 공간에서 발생하는 사건의 수를 모델링하는데 사용되는 Discrete distribution
P(X=0) = b(n,p,0) = q^n = (1-p)^n 이다. 이는 매우 큰 n에 대해 e^(- λ)로 수렴한다.
이를 P(X=k)까지 전개해보자.
P(X=1) = P(X=0)* λ
P(X=2) = P(X=1)* λ
...
P(X=k) = λ^k/k! * e^(- λ) <= Poisson distribution
X: binomial distribution with n,p when n is large and p is small. then X can be approximated as poisson distribution with λ=np.
즉, 빈도가 낮은 사건 p의 발생을 모델링하는데 자주 쓰인다.
ex)
one mistake per 1000 words.
book with 100 words per page.
r.v. S100 = # mistakes on a single page.
(Poisson 근사)

ex)
100 areas( 10*10 blocks )
P(the bomb hits my area) = 1/100
P(400 bombs won't hit my area)
=>

* Important Densities
- Continuous Uniform Density
U가 [a,b] 간격에서 뽑힌 랜덤한 실수라고 가정해보자.
이 U가 f(w) = 1/(b-a) {a<=w<=b}, 0 {otherwise} 의 density function을 지니면 U는 [a,b]에서 uniformly distributed 되었다고 한다.
- Exponential & Gamma Densities
X가 exponential density with a parameter k>0 을 가진다면, X의 density function은
f(x) = ke^(-kx) {x>=0}, 0 {otherwise} 와 같이 정의될 수 있다.
T가 ke^(-kx) 의 density function을 지니는 r.v.라면, T의 cumulative distribute function은 다음과 같이 정의된다.

또한 exponential density function은 "memory less" 특성을 지닌다.
증명)

- Relation between exponential density and Poisson distribution
Xi : (i-1)번째, 그리고 i번째 간격에 사고가 일어남
=> Xi는 exponential density with λ를 지닌다. 또한 X1,X2,...는 i.i.d를 따른다.
Y: 주어진 시간 간격 동안 사고가 일어난 횟수
Sn : X1+X2+...+Xn (n번째 사고가 일어나는데까지 걸린 시간)
P(Y=n)?

따라서 P(Y=n)은 λt를 파라미터로 하는 poisson 분포를 따름을 알 수 있다.
(Sn의 density function의 유도는 다음과 같이 한다.
1. 개별 사건 x의 density function은 exponential하므로 f(x) = λe^(−λx)
2, Sn은 f(x1)+f(x2)+...+f(xn)이다.
3. fSn(x) = f(x1)*f(x2)*...*f(xn)
이 부분부터는 유도 과정이 꽤 복잡하므로 그냥 저렇게 결과가 나온다고 했다.)
결론적으로 시간이 exponential with λ 면서, 사건의 횟수가 정해지고, t의 시간 이내에 일어날 횟수를 따지는 것은 λt를 파라미터로 하는 poisson distribution을 따른다.
*Simulate a poisson distribution with parameter λ
i) 파라미터 λ를 가지는 exponential한 seq.를 생성한다.
ii) Sn<=t<Sn+1을 만족하는 n을 찾는다.(단위 시간 구간 내에 정확히 n개의 사건이 발생함.)
(Sn은 n개의 사건이 발생한 시점이다. 그리고 Sn+1은 n+1개의 사건이 발생한 시점이다.)
*Functions of a random variable
X가 conti. r.v.라고 하고 ϕ(x)가 X의 범위 내에서 strictly increasing function이라고 해보자.
(strictly increasing function은 x1>x2일 시 f ϕ(x1)>ϕ(x2)이다.)
r.v. Y = ϕ(x)이며, Fx,Fy는 X와 Y의 c.d.f.이다.
이때 "Fy(y) = Fx(ϕ^-1(y))"가 성립한다.
만약 strictly decreasing func. 였다면 Fy(y) = 1-Fx(ϕ^-1(y)) 이다.
증명)

=> 따라서 c.d.f. 들을 미분해서 fy(y)를 구할 수 있다.
ex)
Y=x^2, ϕ(x) = x^2
FY(y)?

* Simulation(역변환 샘플링)
- Y는 CDF FY를 가지고 있으며 이는 strictly inc. 함수라고 해보자.
U는 [0,1]에서 uniformly distributed라고 해보자. 그러면 FU(u) = u (0<u<1) 일 것이다.
F(y)=u -> y = F^-1(u) 인 y는 항상 존재한다. (strictly inc기 때문에 F(y)는 0부터 계속 증가할 것이고, 결국 F(y)의 크기가 u가 되는 시점이 있다.)
Z = F^-1(U)로 정의하자. 이런식으로 정의된 Z는 FZ(y) = FU(F(y)) = F(y)를 만족하므로 해당 과정을 통해 같은 distribution을 지닌 새로운 확률 변수를 정의할 수 있다.
=> F(y)가 strictly inc. y의 c.d.f.고 0<F(y)<1 이며, U가 [0,1]에서 uniformly distributed r.v.일 때,
Y = F^-1(U)의 c.d.f. 역시 F(y)이다.
따라서 0~1사이의 Uniform Distribution에서 랜덤한 값을 뽑아서 F(y)의 역함수 F^-1(y)에 대입하면, 임의의 확률 분포 F(y)로부터 무작위 표본을 생성할 수 있는 것이다.
(컴퓨터는 기본적으로 [0,1] 범위의 uniformly distributed 난수만 직접 생성할 수 있기에, 특정한 확률분포에 따른 난수를 얻고 싶을 때 이 방법을으로 간접적으로 구하여 사용한다.)
* Normal Density
- Normal Density func with parameter μ, σ "fx"는 다음과 같이 정의된다.

여기서 μ는 평균(center), σ는 표준 편차(spread)를 의미한다.
c.d.f. Fx of fx는 해당 함수를 적분함으로써 구할 수 있다.
여기서 Z가 μ=0, σ=1의 분포를 따르는 r.v.라면, Z는 "Standard normal r.v."라고 부른다.
만약 r.v. X = σZ+ μ라고 하면, X= ϕ(Z)=σZ+ μ라고 할 수 있다. Z=ϕ^-1(X)이며,
따라서 X = σ ϕ^-1(X) + μ => ϕ^-1(X) = (X- μ)/ σ 임을 알 수 있다.
그렇다면 FX(x) = FZ(ϕ^-1(X)) = FZ((X- μ)/ σ) 임을 알 수 있고,
fX(x)를 구하기 위해 미분을 하면 다음과 같이 된다.

결국 FX(x) = P(X<=x) = P(Z<=(X- μ)/ σ) = FZ((X- μ)/ σ)로 유도할 수 있다.
이제 이에 대해 미리 구해둔 표를 참고해 계산하면 된다.
즉 정규분포를 따르는 X를 변환을 통해 표준 정규분포를 따르게 유도하고 미리 구해진 표를 이용해 계산하는 것이다.
ex)
X : normal r.v. with μ=10, σ=3
P(4<=X<=16)?

'개인 공부' 카테고리의 다른 글
| 데이터 과학 - 5. Data Acquisition (0) | 2024.04.09 |
|---|---|
| 데이터 과학 - 4. Data Mining/Science Algorithms (0) | 2024.04.08 |
| 데이터 과학 - 3.Data Science Methodology Part 2. (0) | 2024.04.03 |
| HCI - Needfinding (0) | 2024.04.02 |
| 데이터 과학 - 2. Data Science Methodology Part 1. (0) | 2024.04.02 |