* Inferential Statistics?
=> 통계적 추론은 우리가 수집한 모집단에서 Sample을 추출해서 진행하는 통계적 데이터 분석 방법이다. 해당 추정 방법에는 Point Estimation, Interval Estimation 방법이 있다.
1. Point Estimate

=> 특정 값을 추정하여 모집단의 parameter를 추정.
2. Interval Estimate

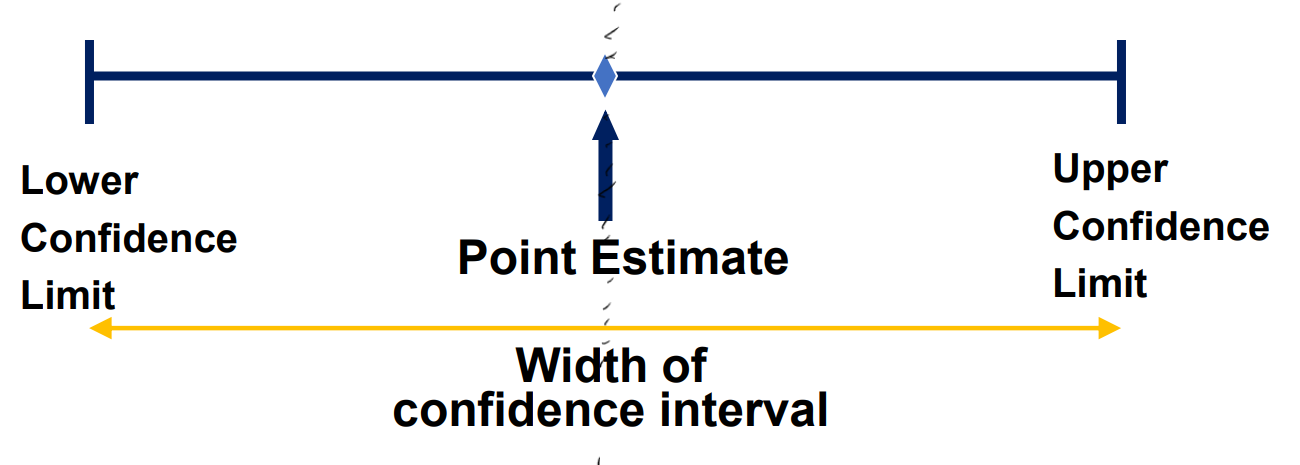
=> 구간을 사용하여 모집단의 patameter를 그리는 방법. 특정 Point를 정의하고 그 Point에서 +-를 하는 방식으로 신뢰 구간을 정하는 것이 일반적이다.
* Biased/Unbiased Estimator

-> 이렇게 해서 추정된 estimator θ'가 E(θ') = θ일 시, Unbiased Estimator라고 하고, E(θ') =/= θ일 시, biased estimator라고 한다. 즉, Unbiased Estimator를 구하는 것이 중요하다. 만약 Sampling된 표본 집단이 모집단의 특성을 골고루 반영하지 못하고 있을 시, Unbiased Estimator가 구해질 확률이 생긴다.(또한 i.i.d. 가정 같은 것이 강하게 위배된 데이터도 위험하다.)
그러면 한번 통계적 추론을 해보는 방법을 알아보자.
* Assumptions for Inference on Mean
-> 우리는 이제 Simple Random Sample을 가지고 있다. 이 Sample의 variable들은 정규 분포를 따르며, 평균(μ), 표준 편차(σ)를 가진다.
이 경우, 우리는 이 SRS로 모집단을 추론할 수 있을까? 일단 우리는 모집단의 평균은 모른다고 가정해보자.
이 때, 케이스는 2가지로 나뉜다.
i) 모집단의 표준 편차를 안다. (사실상 현장에서 이러한 케이스는 거의 없다...)
ii) 모집단의 표준 편차를 모른다.
i) 모집단의 표준 편차를 알 때.
신뢰 구간(CI)은 모집단의 parameter(ex: mean)에 대한 불확실성의 정도를 나타내는 Interval estimate이다. 추정 결과 모집단 parameter가 CI 안에 있을 거라는 의미를 지닌다. 즉, Point estimate를 통해 추정해낸 값 기준 어느정도 구간까지 모집단의 parameter가 존재할 지를 알려주는 정보이다.
신뢰 계수는 제시된 CI 안에 모집단 Parameter가 있을 확률을 표시하는 계수이다.
신뢰 수준(CL)은 신뢰 계수를 퍼센트로 나타낸 것이다.
=> 일반적으로 모든 신뢰 구간은 Point estimate를 통해 추정된 값 θ'을 기준으로
θ' +- (Critical Value)(Standard Error)로 나타낸다. Critical Value는 우리가 원하는 CL을 맞추기 위해 세팅하는 값이며 SE는 point estimate의 표준 편차이다.
1. 모집단에서 size n 만큼의 표본을 추출한다.
2. 해당 표본 집단의 평균
μ'를 계산한다. (이 때 ,표본이 정규 분포를 따르게 제대로 추출되었나를 분석한다.)3. μ'를 표준 정규 분포를 따르게 변환한다. 
4. Z는 표준 정규 분포를 따르므로 해당 값을 통해 추정을 할 수 있다.
이러한 과정을 통해 추론을 σ를 알 때 Confidence interval etimate는 다음과 같다.

-> za/2는 Crit. Val. 이며 이는 사전에 정의되어있는 score 표가 있다.

따라서 만약에 양쪽으로 신뢰구간 0.95를 사용하고 싶다면, +-1.96을 사용하면 된다.
여기서 명심해야할 것은 모집단의 parameter는 고정되어있고 우리는 그 고정값을 추정하는 것이기 때문에, "95%의 신뢰도로 해당 구간이 μ를 포함할 것이다."는 맞는 표현이나, "μ가 95%로 해당 구간에 놓일 것이다."는 틀린 표현이다.

=> 이 사진을 통해 95% 정도 표본 평균을 기준으로 한 신뢰 구간이 모 평균을 캡처한다는 뜻을 이해하면 편하다.
ii) 모집단의 표준 편차 σ를 모를 때.
Main Idea : 기존 Z 추정에서 모집단의 표준 편차 대신 Sample의 표준 편차 σ'를 넣되, Z-distribution이 아닌 T-추정의 T-distribution을 사용하자. (만약 모집단이 정규 분포를 따르지 않는다면, n>30 이상의 큰 sample을 사용하자.)
- t 분포 추정의 방법에는 다양한 방법이 있지만, Single value estimate는 Student's t distribution을 사용하면 된다.

=> 기존 point estimator + (crit.Val.)(SE) 에서 z가 t로 바뀌며 degree of freedom이 추가 parameter로 붙은 것, 모표준편차 σ의 값이 표본표준편차 s로 바뀐 것이 차이이다.
=> Student's T distribution에서 degrees of freedom(d.f.)는 "n-1"이다. (n : size of sample)
ex : X1,X2,X3의 평균이 8일 때, X1,X2는 어떤 값을 가져도 상관이 없다. 예를 들어, X1 = 10000, X2 = 20000 이어도 된다.
그러나, X1,X2를 확정함으로 인해, X3의 값은 자연스럽게 "고정"된다. 이를 degrees of freedom이라고 부르며, 자료의 수가 3이므로 3-1 = 2가 d.f.가 된다.
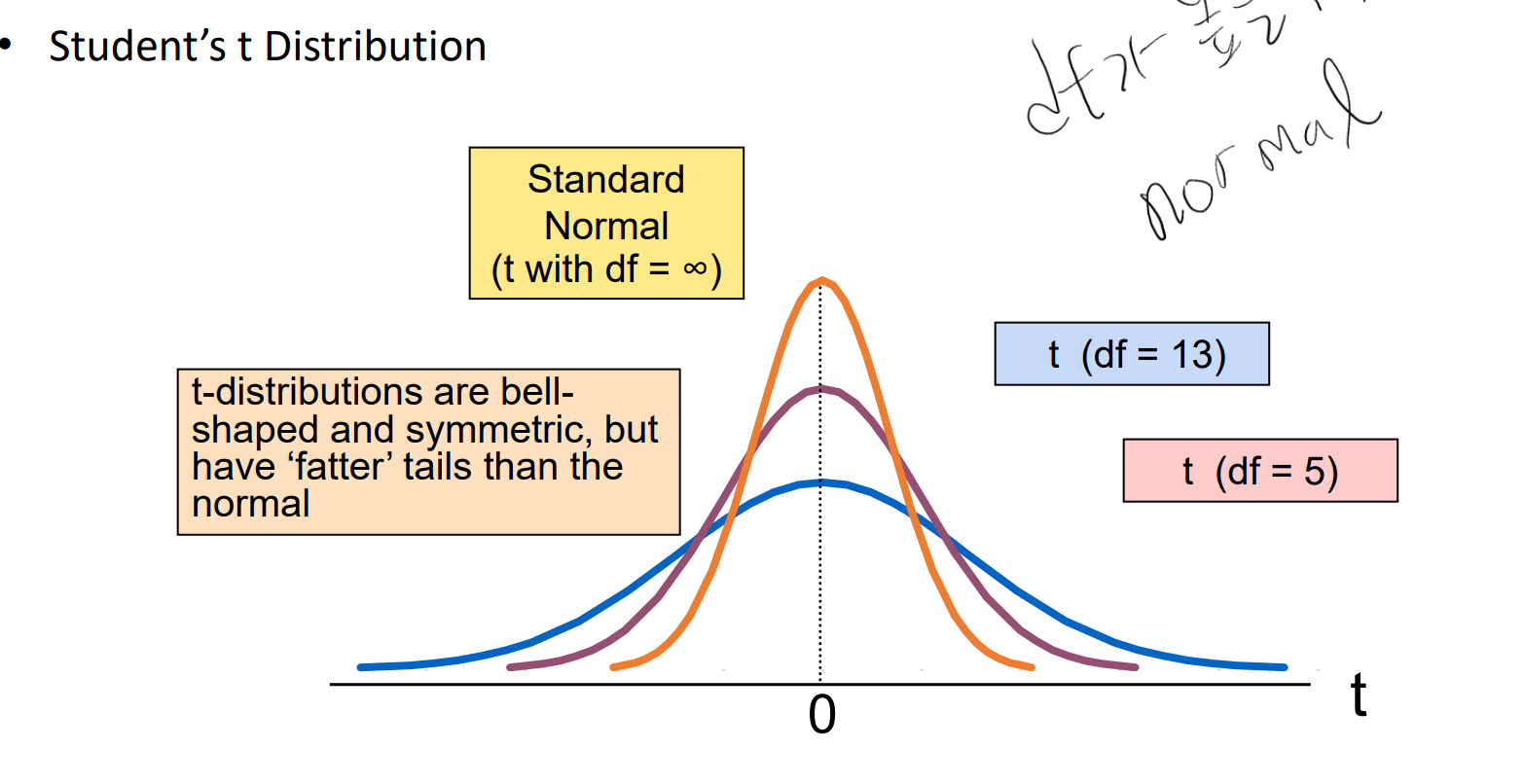
=> T 분포는 d.f.가 높을수록 normal distribution과 비슷해진다. 따라서 충분히 큰 d.f.의 t distribution은 그냥 z dstribution으로 근사해서 사용해도 된다.
=> T-분포는 모집단이 정규 분포를 따르지 않더라도 sample 크기가 클 경우 일반적으로 robust 한 특성이 있다.
* 독립 시행에서의 통계적 추론
-> data가 정규분포를 따를 때, 추출한 표본 n개의 데이터 중 x개 success일 시, p=x/n, q=1-p로 정의할 수 있다.
여기서 모집단의 비율 π를 추정하기 위해서는 표준 편차를 sqrt(p(1-p)/n) 으로 가지는 추정을 하면 된다.
(확률과 통계 내용 참고)


ex)
random sample 100 개중 25개가 성공이라고 해보자.
그러면 p=0.25, q = 0.75 이고 이를 95% 신뢰도로 추정을 해보면,
CI는 0.25 +- 1.96*sqrt(0.25*0.75 / 100) = 0.25+-1.96(0.0433) 임을 알 수 있다.
즉 모집단의 proportion π는 0.1651<= π <= 0.3349 로 캡처 가능함을 알 수 있다.
* Determining Sample Size
- 그렇다면 모집단에서 얼마만큼의 샘플링을 해야 좋을까?

이 부분이 신뢰 구간을 정하는 계수이다. 그리고 우리가 원하는 Sampling error rate을 e라고 해보자.
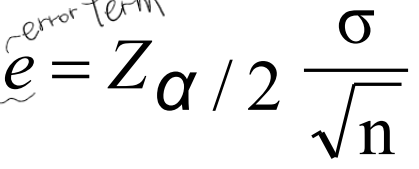

다음과 같은 유도로 원하는 error rate에 따른 필요 샘플링 양을 계산할 수 있다.
ex)
σ = 45 일 때, 90%의 confidence로 5의 error rate을 지니는 추론을 하고 싶다.
n = (1.645)^2 * 45^2 / 5^2 = 219.19
따라서 220개의 sampling을 해야한다.
만약 σ를 모를 때는 그냥 t 분포로 계산해도 된다.

이 때는 추출된 n 값에 따라 d.f.가 변하므로, 변한 d.f.에 맞춰 재계산된 t val을 대입해 계속 계산한다. 그러다가 n의 값이 변화가 없으면 해당 n 값을 사용한다.
* 가설 검정
-> 기존에 존재하던 사실 (H0)를 가정하고 이를 반박하는 가설 (Ha)를 세운 후, p-value를 계산하여 H0을 기각할 지 판단하는 검증법.
1. 가설, 가정 설정
- Null hypothesis (H0) : 표본으로 추출한 데이터가 모순된 지표를 가리키지 않는 한, 참인 가설(기본적인 환경)
- Alternative hypothesis (Ha) : H0의 반대. 보통 우리가 입증하고 싶어하는 가설.
=> 이 때, H0 or Ha 외의 상황은 없어야한다. (그래야 H0를 기각시 Ha가 참이 된다.)
H0, Ha를 정하고 Siginificance level a를 정한다.
2. Test Statistic 계산
- 추출한 표본에서 Z-stat, T-stat, Chi-square 등을 계산한다. 이 값은 sample이 얼마나 null hypothesis에 가까운지를 설명한다.
3. P-value : Sample에서 statistic 계산을 통해 유도된 H0에 대한 확률 측도. 해당 값을 통해 H0의 기각 여부를 결정 가능하다. p-val이 정해둔 significance level(a)보다 클 시, H0을 기각하지 못하고, 작을 시 기각할 수 있다.
ex:
남자의 키 데이터가 있다고 가정하자. 거기서 우리는 모평균이 170이고, 모표준편차가 40이라는 것을 알고있다고 하자.(Z-stat). 64개 만큼의 Sample을 추출했더니, 표본 평균 x' = 185 였다고 하자.
Zstat = (185-170)/ (40/sqrt(64)) = 14/5 = 3.

표준 정규 분포표에 의하면 Zstat이 3일 때, 0~3까지 적분한 값이 0.4987임을 알 수 있다. 따라서 0.5-0.4987 = 0.0013 이다. (H0이 true라면, 해당 표본이 잘못된 것이고, H0를 중심으로 가지는 정규분포 표에서 범위 밖에 있을 것이다.)
이 때, 우리의 H0가 남자의 평균 키가 170이다. 이고, Ha가 남자의 평균 키가 170이 아니다. 라고 가정하자.
이 경우, 정규 분포표의 양쪽을 봐야한다.(170보다 큰쪽, 작은 쪽 두개가 표함된다.)
즉, 0.0013*2 = 0.0026이 된다. crit. val.을 0.05로 세워뒀을 때, 0.05>0.0026이다. 따라서 H0를 강하게 기각할 수 있다.(남자의 모평균은 170이 아니다.)
* 가설 검정의 에러.
=> 에러에는 2가지 타입이 있다.
1. H0이 사실인데 기각했다.
2. H0이 거짓인데 기각을 하지 않았다.

b가 Type II error가 일어날 확률일 때, power는 1-b이다. (Type II error를 피할 확률)
즉, power 값이 크면 Type II를 피할 수 있다.
significance value "a"와 다르게 b는 자동으로 정해진다. a와 b는 Trade off 관계에 있으며, a가 엄청 작을 경우 대부분의 H0를 기각하지 않게되어 Type II error rate이 올라가게 된다. 그러나 a가 너무 클 경우, 대부분의 H0를 기각하게 되어 Type I error가 많아지게 될 것이다. 즉, 2개의 error를 잘 다루는 것이 중요하다. (sample size가 커져도 power는 증가한다.)

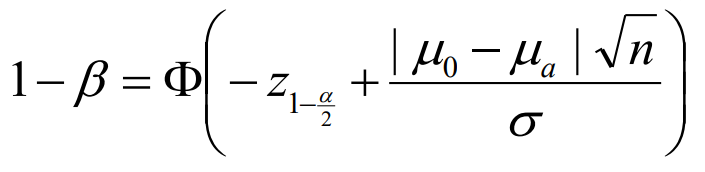

-> Φ는 표준 정규 분포 Z의 누적 분포 확률(적분 값) 이다. Power의 정의란 H0이 거짓이면 reject할 확률이다. z(1-a/2)는 H0이 false일 경우이다. H0이 false일 경우, power는 reject 해야하고, 따라서 바깥부분의 적분 값을 구하는 것이다.

=> 결국 H0이 참일 때 분포(상단), Ha가 참일 때의 분포(하단)의 정규 분포를 생각해보면 쉽다. 하단 곡선이 189.6을 초과할 확률은 0.5160이므로, power는 51.6%임을 의미한다.
따라서 power까지 고려한 samling size는 다음과 같이 계산 될 수 있다.

* Chi-square test
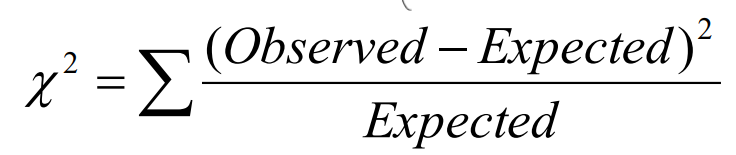
=> 큰 Chi-square 일 수록 두 개의 variable들이 연관되어있을 확률이 높다.

이런 데이터가 있을 때, 다음과 같이 chi-square 값이 계산된다.

chi-square test에서 Degree of freedom은 (row-1)(col-1)로 계산이 가능하고, 정해진 significance threshold보다 chi value가 작을 시, 기각한다.
'개인 공부' 카테고리의 다른 글
| 데이터 과학 - 11. Clustering (0) | 2024.04.25 |
|---|---|
| 데이터 과학 - 10. Association Rule Mining (0) | 2024.04.24 |
| 데이터 과학 - 9. Statistical Data Analysis PART 1 (0) | 2024.04.19 |
| 데이터 과학 - 8. Data Preprocessing Part 2 (0) | 2024.04.18 |
| HCI - Safety (0) | 2024.04.16 |