* Law of Large Numbers for Discrete Random Variable
* Markov's inequality
X가 P(X>=0) = 1인 r.v.일 때, 모든 t>0에 대해, P(X>=t) <= E(X)/t
* Chebyshev Inequality
X = discrete random variable with expected value µ=E(X), and let ε>0 be any positive real number.

ex)
E(X) = µ, V(X) = σ^2 인 r.v. X에 대해 ε=kσ (k>0) 이라고 잡고 Chebyshev Inequality를 적용하면,

이와 같이 정리가 된다.
따라서 임의의 constant를 잡을 때, bound 값을 σ와 무관한 값으로 잡고싶을 때, kσ와 같은 값을 앱실론으로 잡으면 된다.
ex)
한 population에서 추출한 n random sample(X1,...,Xn)이 있다고 할 때(i.i.d.를 따른다.), 역으로 random sample에서 µ와 σ를 알아내기. (단, σ^2<2 이다.)
Q. # samples to satisfy P(|An- µ|<1)>=0.99?

ex)
X - r.v.
Px - distribution function of X
Px(- ε) = 1/2, Px(ε) = 1/2. ε>0.
E(X) = 0, V(X) = ε^2.

이때, µ=0이므로, P(|X|>= ε) <= 1.
* Law of Large Numbers (LLN) - Weak
X1,...,Xn = i.i.d.
E(Xi) = µ, V(Xi)=σ^2.
r.v. Sn = X1+X2+....+Xn, An=Sn/n
E(An) = µ, V(An) = (σ^2)/n
이 때, n이 커지게 되면 An은 어떻게 될까?
=> 임의의 ε>0 인 ε에 대해, P(|An- µ|>= ε) -> 0으로 수렴한다.
따라서 P(|An-µ|<ε) -> 1이다.
즉, n이 무한대로 커지면 An = µ가 된다. (즉 population에서 많은 sampling을 하면 An은 당연히 모집단의 평균 µ에 수렴한다.)
따라서 population에서 n개의 random sample을 뽑았을 때 E(An)= µ이며, P(An-> µ) -> 1로 수렴한다.
* LLN - Strong
lin(n->inf.) P(An = µ) = 1이 된다.
즉, Weak는 확률이 1로 수렴한다는 것이고, Strong은 An=µ일 확률이 1이라는 것이다.
ex) Roll a die
r.v. Xj : jth outcome
Sn = X1+X2+...+Xn
E(Xi) = 7/2
이때, LLN에 의해 P(|An-7/2|>= ε) -> 0이다.
즉 Xi를 수없이 시도하면(i->inf.) An -> 7/2 일 것이다.
ex)
X1,...,Xn : Bernoulli trials with p=0.3
E(Xj) = 0.3*1 + 0.7*0 = 0.3
V(Xj) = pq = 0.21
E(An) = 0.3
V(An) = 0.21/n
by Chebyshev inequality, P(|An-0.3|>=ε) <= (0.21/n)/ε^2.
이 때 ε=0.1 이라면, P(|An-0.3|>=0.1) <= 21/n
즉, P(|An-0.3|<0.1) >= 1-(21/n)
n=100 일 때, P(0.2<An<0.4)>=0.79이다.
즉 성공 확률 p=0.3인 Bernoulli trial을 100번 하면 An이 0.2~0.4 사이에 있을 확률이 0.79이다.
* Law of Large Numbers for Continuous Random Variable
*Chebyshev Inequality

X가 conti. r.v. 여도 똑같이 적용된다.
* LLN - Weak
n이 매우 클 때 다음이 성립한다.

ex) Uniform Case
X1,...,Xn : i.i.d. from uniform density on the interval [0,1]


그러므로 Chebyshev inequality에 의해 모든 양수 ε에 대해 다음이 성립한다.
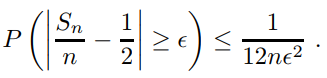
ex) Standard Normal Case
X1,...,Xn : i.i.d. from Standard Normal (µ=0, σ=1)
=> E(Xi) = 0, V(Xi) = n
E(An) = 0, V(An) = 1/n
by Chebyshev inequality에 의해

* Monte Carlo Method
x^2+y^2<=r^2 과 같은 원의 방정식의 넓이를 구할 때, x,y를 무작위로 뽑아서 x^2+y^2<=r^2을 만족시킬 때만 x,y count를 증가시키면, 이 count가 원의 넓이에 가까워진다.(π*r^2)
=> g(x)를 [0,1] 사이에 정의되는 conti. function이며 값도 [0,1] 사이에 정의된다고 하자.
또한, x는 0~1사이에서 uniform distribution에서 뽑힌 값이므로, Yi=g(x)인 E(Yi)는 다음과 같이 정의될 수 있다.


An = (Y1+Y2+...+Yn)/n = area의 average이며, n을 매우 많이 추출할 시, 넓이에 수렴한다.
(E(An)=µ이고, µ=E(Yi)= g(Xi)*f(x)를 0~1 적분한 값이다. 즉, µ=넓이 이다.)
이 때, V(Yi) = E((Yi- µ)^2) 이고, Yi는 [0~1]에서 정의되고, µ도 [0~1]로 정의되므로 V(Yi)는 finite하다.(0<=V(Yi)<=1)
그러므로 V(An) = σ^2/n 으로 두고, Chebyshev inequality를 적용하면,

이 정의된다. 즉 g(x) 또는 Yi를 추출한 횟수 n에 따라 An과 실제 넓이와의 오차를 ε 범위 내에서 조절이 가능하다.
*p.s. 작성하다보니 계속 빼먹었는데, Markov는 E(X)만, 나머지 경우는 V(X)도 정의될 경우에만 성립한다.
'개인 공부' 카테고리의 다른 글
| 확률 및 통계 - 10. Generating functions (0) | 2024.05.24 |
|---|---|
| 확률 및 통계 - 9. Central Limit Theorem (CLT) (0) | 2024.05.23 |
| 확률 및 통계 - 7. Sums of Independent Random Variables (0) | 2024.05.07 |
| 데이터 과학 - 12. Clustering Part 2(DBScan) (0) | 2024.04.27 |
| 데이터 과학 - 11. Clustering (0) | 2024.04.25 |


