10.1. Generating functions for Discrete distributions
평균과 분산만으로는 분포에 대한 모든 정보를 알 수 없다.
* Moments
μk : k-th moment of X
μk = E(X^k)

ex) μ = E(X) = μ1, σ^2 = E(X^2) - (E(X))^2 = μ2 - ( μ1)^2
=> 정의된 X에 대한 모든 moment들을 알면 X에 대한 분포를 정의할 수 있다.
* moment generating functions(m.g.f.)


Ex)
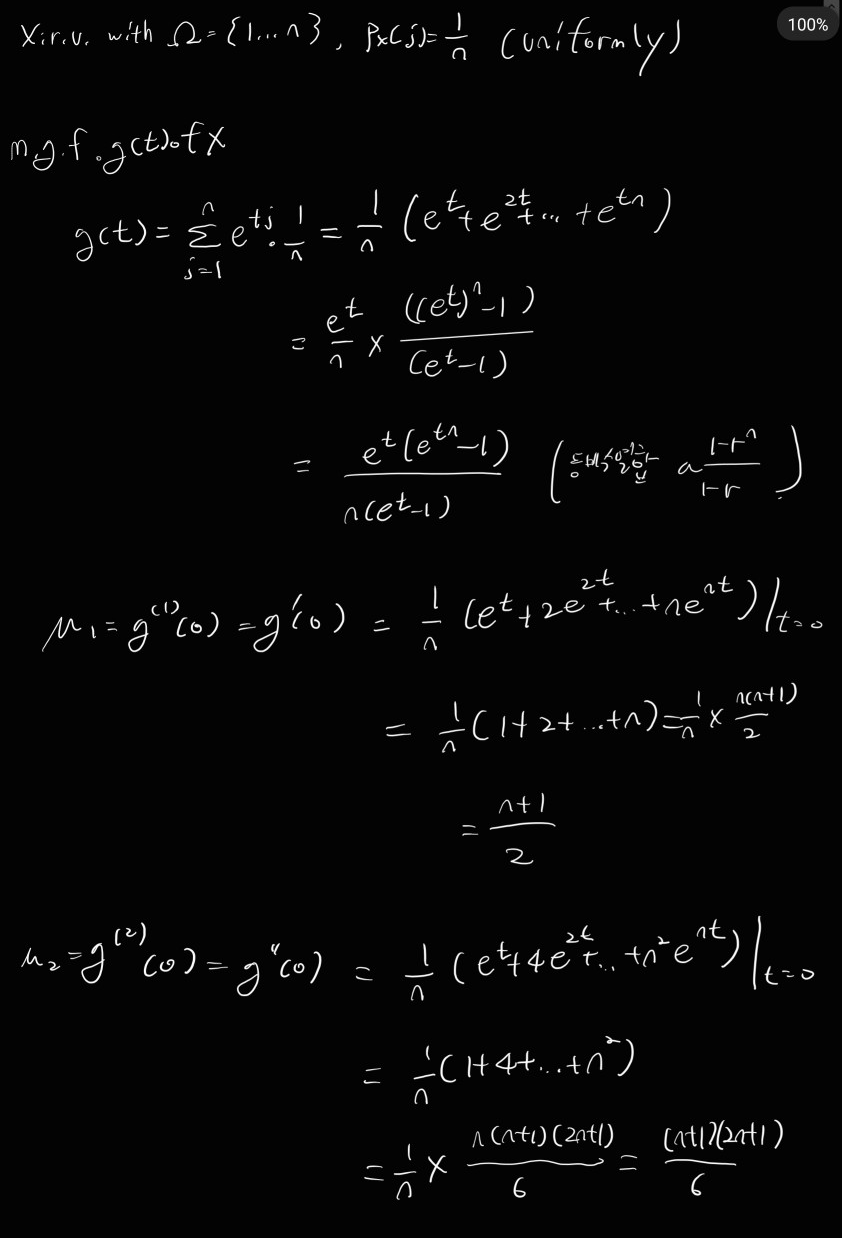
* Moment Problem
X가 유한한 Sample Space의 discrete r.v.이고 moments µk = E(X^k) 이면, 다음의 정리가 모든 t에 대해 수렴한다.
=> 어떤 분포 p로 정의되는 g(t)에 대해, g(t)가 결정하는 p는 유일하며, 그 반대의 경우도 성립한다.
(Moment를 구함으로써 분포를 표현할 수 있는 이유)
* Ordinart generating functions
Sample space가 non-negative integer들이라고 하자. ({0,1,2,...})
그리고 이 Sample space에서 정의되는 r.v. Xj = j라고 하자.

그렇다면 해당 Xj의 분포에 대한 moment generating function은 다음과 같이 정의될 수 있다.
여기서 e^t를 z로 치환하면 다음과 같이 z에 대한 polynomial h(z)를 정의할 수 있다.

그렇다면 다음의 관계가 성립한다.

g(0) = h(1), µ1 = g'(0) = h'(1), µ2-µ1 = g''(0) - g'(0) = h''(1)임을 알 수 있다.
* Properties
X가 discrete r.v.이고 Y가 X+a (a = constant)라면 m.g.f of Y gy(t)는 다음이 성립한다.

만약 Y가 bX 였다면 다음이 성립한다.



만약 X,Y가 독립 r.v.면서 Px, Py의 distribution function을 지니고, Z = X+Y라면, e^tx, e^ty도 독립일 것이고, E(e^tx*e^ty) = E(e^tx)E(e^ty)로 표현이 가능하다. 따라서 gz(t),hz(t)는 다음과 같이 정의된다.

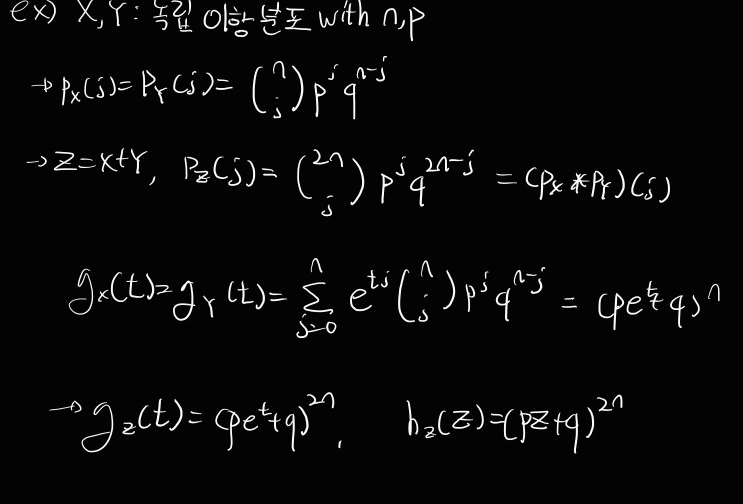
=> hz(Z), gz(t)를 통해 Z(X+Y)도 역시 이항 분포를 가짐을 알 수 있다.
'개인 공부' 카테고리의 다른 글
| CLIP : Connecting text and images. (기본 개념) (0) | 2024.06.25 |
|---|---|
| Q-Learning (0) | 2024.06.24 |
| 확률 및 통계 - 9. Central Limit Theorem (CLT) (0) | 2024.05.23 |
| 확률 및 통계 - 8. Law of Large Number (0) | 2024.05.07 |
| 확률 및 통계 - 7. Sums of Independent Random Variables (0) | 2024.05.07 |

