X1,...,Xn이 평균을 μ, 분산을 σ^2 으로 지니는 i.i.d. 조건 분포에서 random sampling(independent trials)되었다고 생각해보자.
Sn = X1+X2+...+Xn, An = (Sn)/n 이다.
이 때, 이전까지 증명했던데로 다음의 2가지는 자명한 사실이다.
1. E(An) = μ
2. n을 무한으로 늘리면 An -> μ
그렇다면 An(Sn)의 분산은 매우 큰 n에 대해 어떻게 변하게 될까?
1. Ø(x) : x를 가지는 standard Normal density function.

2. NA(a*,b*) = Ø(x)를 a*~b* 구간에서 적분한 값.
9.1. Central Limit Theorem for Bernoulli trials
성공 확률이 p인 베르누이 시행은 Sn = b(n,p,j) = P(Sn>=j), E(Sn) = np, V(Sn) = npq 이다.
이 때, 이 Sn을 Standarized sum을 통해 E(Sn*) = 0, V(Sn*) = 1로 변환해준다.


* binomial distribution의 CLT는 다음과 같다.

Ex)
55 heads in 100 tosses of coin.
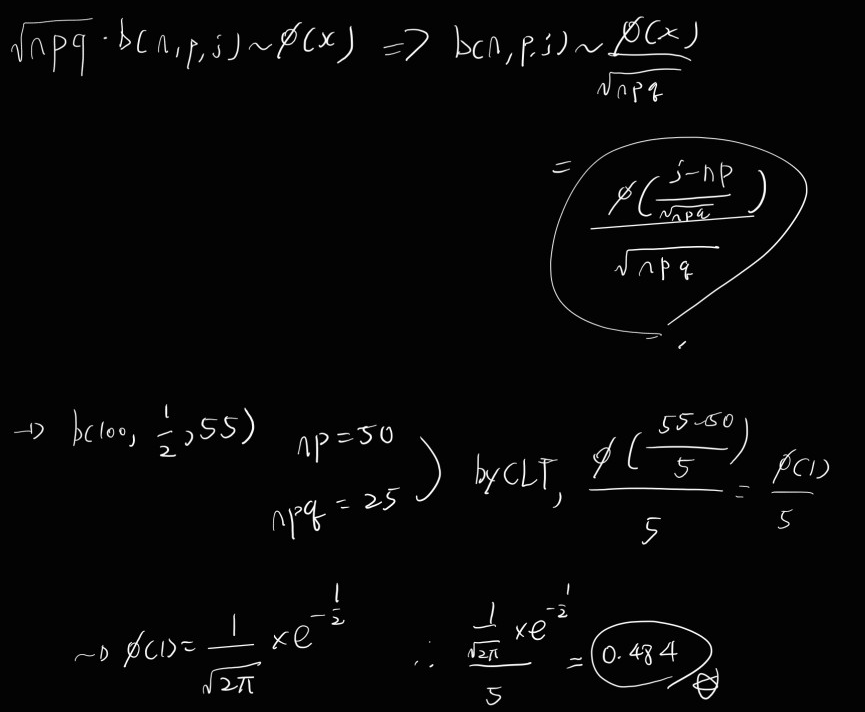
Sn : The number of sucesses in n Bernoulli trials with parameter p.
이 때, 이 Sn을 a,b 사이에 바운드 되는 확률이라고 하자. 이를 Standarized sum을 하여 나타내보면 다음과 같다.

Ex)
Coin toss 100 times, P(40<=Sn<=60)?

성공 확률 p의 Bernoulli trial에서, Sn의 추정식은 다음과 같다.

더 일반적으로 설명하자면, 특정 모집단에서 추출한 표본들의 평균 An을 위의 사진과 같은 과정으로 바운딩할 수 있다는 것이다.
Ex)
만약 사진에서 β=2, α=0.954 라면, Critical interval의 길이를 0.06으로 만드는 최소 추출 수는?

9.2. Central Limit Theorem for Discrete Independent trials
(위의 Bernoulli version과 거의 비슷하게 진행된다.)
X1,...,Xn : i.i.d 일 때, E(Xi)= μ, V(Xi) = σ^2이며 E(Sn) = nμ, V(Sn) = n*σ^2, E(An) = μ, V(An) = σ^2/ sqrt(n)이다.
이를 Standardization하면 Sn*는 다음과 같이 변환된다.

그리고 이 함수는 1/sqrt(n*σ^2) 만큼의 간격을 지닌다.

=> 이 때, 이렇게 Standardization을 한 Sn*를 통해 표준 정규 분포표로부터 적분 값을 구할 수 있다.

Ex) Roll a die 420 time.
P(1400<=Sn<=1550)?

Ex) Grades in 30 Courses ( each course has 100 possible integer points.)
error in grading with k(points) with prob. (1/(20*|k|)p. (k= (-5~5) integer)
P(no error) = 1 - (137/(30))*p
Difference between correct average grade and the recorded average grade is less than 0.05?

* A more general CLT
=> i.i.d(독립이며 동일한 분포에서 추출됨을 의미)를 가지는 Xi들에 대해
Sn: Xi들의 합
E(Xi) = μi, V(Xi) = σi^2, E(Sn) = mn, V(Sn) = sn^2 이라고 해보자. 이 경우 다음이 성립한다.

9.3. CLT for Continuous Independent Trials
Sn = X1+X2+...+Xn이라고 하고, Xi는 i.i.d. 조건을 만족한다 했을 때, E(Xi) = μ, V(Xi) = σ^2 이라고 해보자.
그러면 다음이 성립한다.

Ex)
measure of distance 1. μ = 1, σ = 0.0002.
measure n times, take the average. (measurements are mutually independent)
Q. The number of measurements to satisfy the average lies with in 0.0001 of the true value?


* Estimating the Mean
랜덤 추출한 표본의 평균(μ')= Sn/n.
이때 표본의 평균을 가지고 모평균을 추정해보자.
n=36, P(|An- μ|<0.00002) ~ 0.997
=> E(μ') = μ, P(|μ'-μ| < 0.0002) ~ 0.997
=> P(μ'-0.0002 < μ < μ'+0.0002) ~ 0.997
=> 99.7% Confidence interval of μ
(모 표준편차는 알고있다고 가정)
* Sample Variance
모 표준편차도 모르고 모 평균도 모를 때, 우리는 표본들에서 표본 표준편차를 구해서 사용해야한다.

이 때, 우리는 T-value를 사용한다.

이 때 자유도(degree of freedon) = n-1이다.
* 자유도 : a+b+c = 5 일 때, a,b가 자유롭게 결정되면 c는 자동으로 고정된다. 이것이 자유도이다.
'개인 공부' 카테고리의 다른 글
| Q-Learning (0) | 2024.06.24 |
|---|---|
| 확률 및 통계 - 10. Generating functions (0) | 2024.05.24 |
| 확률 및 통계 - 8. Law of Large Number (0) | 2024.05.07 |
| 확률 및 통계 - 7. Sums of Independent Random Variables (0) | 2024.05.07 |
| 데이터 과학 - 12. Clustering Part 2(DBScan) (0) | 2024.04.27 |