1. Introduction
* Dependability
Component가 서비스를 client에게 제공하기 위해, 다른 Component의 서비스에 의존할 수도 있다. 즉, 하나의 component는 완전히 독립적으로 동작하지 않을 수도 있으며, 다른 component와의 상호작용에 따라 동작이 달라질 수 있다.
정의 : component C가 component C*에 의존한다고 할 때, C*의 동작이 올바르게 수행하지 않으면 C 역시 장애가 발생한다. (여기서 component는 프로세스나 채널을 의미한다.)
=> 이러한 Dependability의 요구사항은 크게 4가지가 존재한다.
1. Availability : 시스템의 사용 가능 상태가 얼마나 잘 유지되는지를 의미.(얼마나 준비상태를 유지할 수 있는지.)
2. Reliability : 서비스 상태가 중단되지 않고 얼마나 지속될 수 있는가를 의미.
3. Safety : 시스템이 문제를 일으킬 가능성이 얼마나 낮은지를 의미.
4. Maintainability : 시스템이 장애를 일으켰을 때 얼마나 쉽고 빠르게 복구될 수 있는지를 의미.
* Reliability vs Availability
- Reliability R(t) of component C 정의 : component C가 T=0에서 정상적으로 작동하고 있을 때, 주어진 시간 구간 [0,t) 동안 정상적으로 작동할 확률.
- Reliability metric
1. Mean Time To Failure : component가 실패하기까지 걸리는 평균 시간
2. Mean Time To Repair : component가 실패에서 회복하기까지 걸리는 평균 시간
3. Mean Time Between Failures : MTTF+MTTR
- Availability A(T) of component C 정의 : 주어진 시간 간격 [0,t)동안 component C가 정상적으로 작동 가능한 상태의 비율.
(A(∞) = Long-term availability)
- Availability 수식 : MTTF / MTBF
=> 즉, MTTF가 클 수록 실패까지 걸리는 시간이 늘어나고, MTTR이 작을 수록 복구까지 걸리는 시간이 줄어든다는 의미이다.
* Failure vs Error vs Fault
1. Failure : component가 요구된 사양을 만족하지 못하는 상태.
2. Error : Failure로 이어질 수 있는 component의 일부 결함.
3. Fault : Error를 발생시키는 원인.
=> 즉 Fault가 발생하여 Error가 일어나고 이것들이 Failure를 유발하는 것이다.
* Handling faults
1. Fault prevention : fault가 발생하지 않도록 사전에 예방하기
2. Fault tolerance : fault가 발생해도 시스템이 유지되도록 설계하기
3. Fault removal : 이미 존재하는 fault를 제거하기
4. Fault forecasting : 현재 존재하는 fault, 미래 발생 가능성, 영향을 예측하기.
* Redundancy for failure masking : Redundancy는 시스템에서 failure가 발생하더라도 이를 감지하거나 복구하기 위한 방법.
1. Information redundancy : data unit에 추가 비트를 추가하여 Error가 발생했을 때 이를 복구하는 방법.
2. Time redundancy : 시스템이 Error가 발생했을 경우 동일한 작업을 반복하여 처리하는 방법.
3. Physical redundancy : 여러개의 동일 작업 component를 구성하여 single point failure를 해결하는 법.
2. Fault tolerance in distributed storage systems
* Redundancy in distributed storage systems

- (n, k) MDS Codes : 총 n개의 노드 중 k개의 노드만 있으면 원본 파일을 복구할 수 있는 방식
1. 파일 크기 M을 노드 크기 만큼 분할.
2. 분할된 데이터 조각에 redundancy를 추가 하여 새로운 데이터 조각 생성. (인코딩)
3. 노드에 분할 저장. (각 노드는 M/k 단위의 데이터를 저장)
- 결함 노드 발생 시

기존 repetition code는 노드가 실패 시 백업 노드에서 그대로 가져와 복구 한다. 그러나 (n, k) MDS는 2개의 노드에서 중복성을 제거하여 복구를 한다.

MDS 방식은 기존 방식에 비해 Reliability가 높다. 그러나 Repair의 cost는 올라가므로 Repetition code는 high efficient, low reliability. MDS code는 low efficient, high reliability라고 이해하면 된다.
- Straggler effects : 분산 컴퓨팅 환경에서 시스템의 일부 노드가 다른 노드에 비해 작업을 느리게 처리하면 어떻게 될까?

Task 2, 3 은 Task 1을 처리하는 노드에 비해 빠르게 완료되었지만 Task 1 node를 기다려야 하는 현상이 발생한다.

고 지연 이벤트가 자주 발생할 때, 서버의 갯수가 늘어나면 늘어날 수록(대규모 시스템) 치명적임을 알 수 있다.
따라서 Straggler effects는 시스템이 커지면 커질 수록 치명적임을 알 수 있다.
* Response time에 변동성이 생기는 이유
1. Shared Resources contention
2. Background Daemons (특정 노드가 Coordinator 등 추가적인 백그라운드 업무를 수행할 때 해당 프로세스가 작업 속도를 저하시킴.)
3. Global resource sharing
4. Maintenance Activities
5. Queueing
6. Power Limits : 노드가 PSM에 있을 경우
7. Garbage collection : 노드가 메모리 정리 중에 있을 경우
8. Energy management
=> 즉, 노드의 에너지(computing power) 자체가 내려가거나, 별도의 업무를 추가 수행하거나, 자원 경쟁 문제 등 때문에 변동이 생길 수 있다.
- Straggler modeling : 각 worker node의 계산 시간(Tw)이 지수 분포를 따른다고 가정할 시, 시간 t 이하에서 작업이 완료될 확률은 다음과 같다.
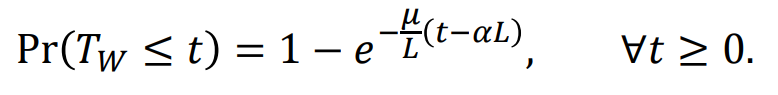
* Mitigating straggler effects : 그렇다면 어떻게 Straggler Effect를 줄일 수 있을까?
=> Straggler effect와 computation load는 Trade-off 관계이다. 즉, 계산양이 많지 않으면 자연스럽게 부하가 줄어들고, 계산 요구량이 많아지면 부하가 걸리는 것이다.
- Redundancy in distributed computing
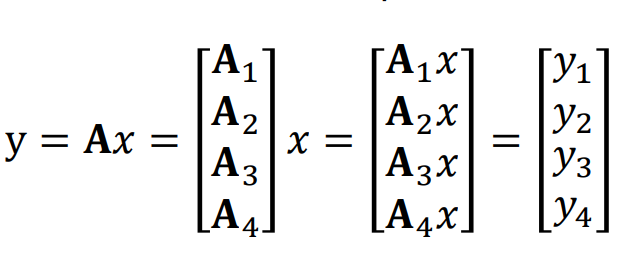
예를 들어, 이러한 행렬 곱을 한다고 생각해보자. 이 때, 행렬을 행 단위로 나누어 각 행을 A1,A2,A3,A4로 분할하고 각 Worker 노드에게 곱셈을 시킬 수 있다.(uncoded)
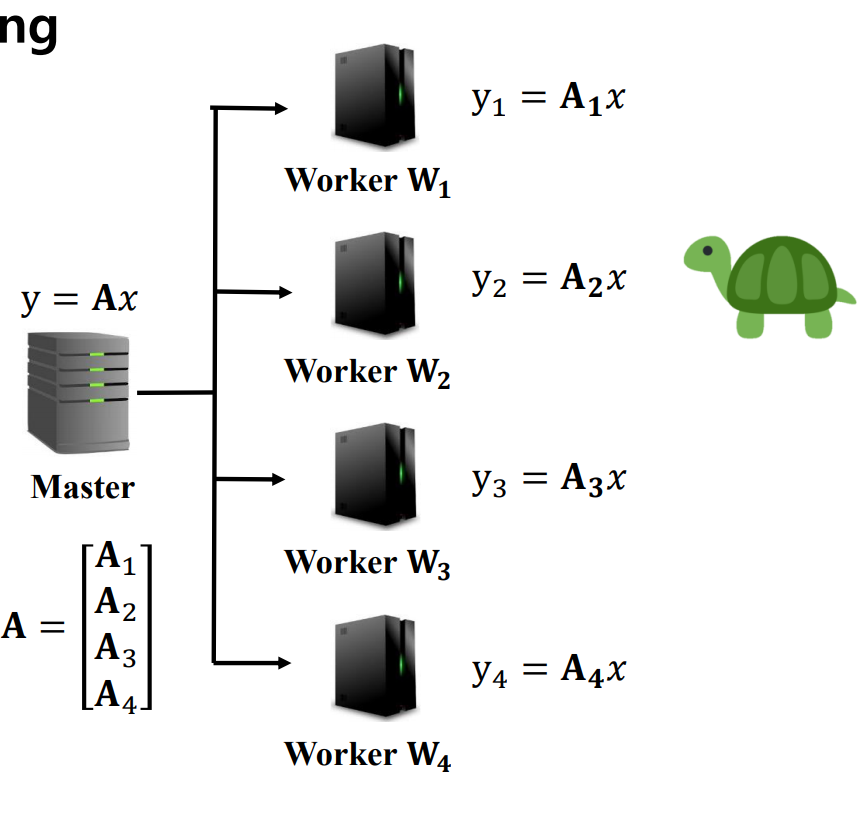
이 경우, 전체 작업 완료 시간은 가장 처리가 느린 W2의 시간이 될 것이다. 또한 Computation load는 단일 노드가 계산하는 것에 비해 1/4가 될 것이다.
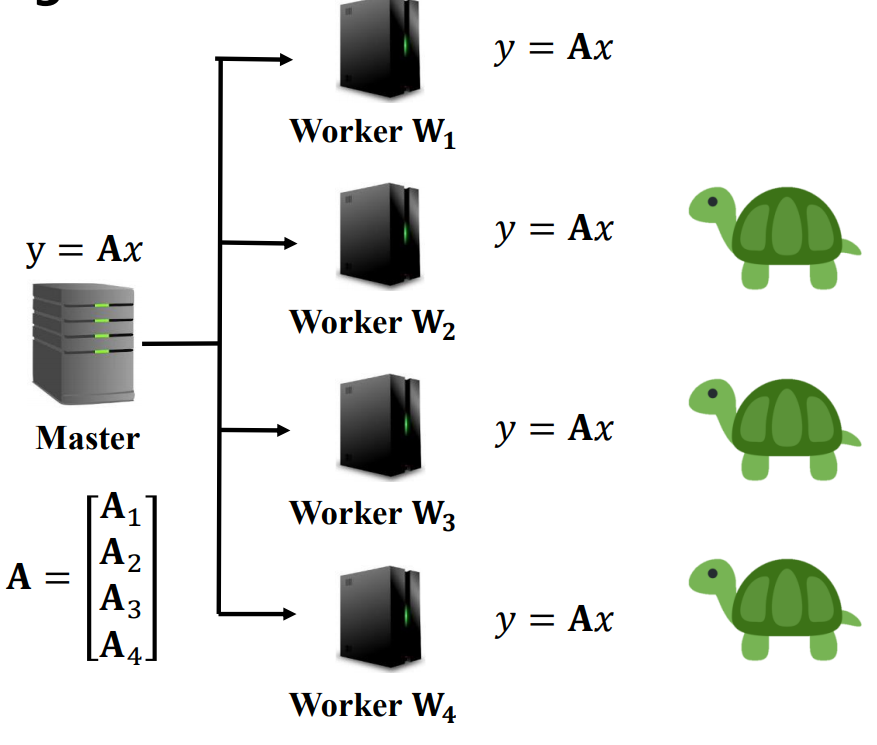
이를 접근 방법을 바꾸어 Ax 라는 행렬곱 자체를 각 Worker에 동일하게 시킨다고 해보자. 이 때 작업 완료 시간은 가장 빠른 W1의 시간이 되고, 각 worker에게 Computation load는 온전히 total computation load가 걸릴 것이다.(repetition)
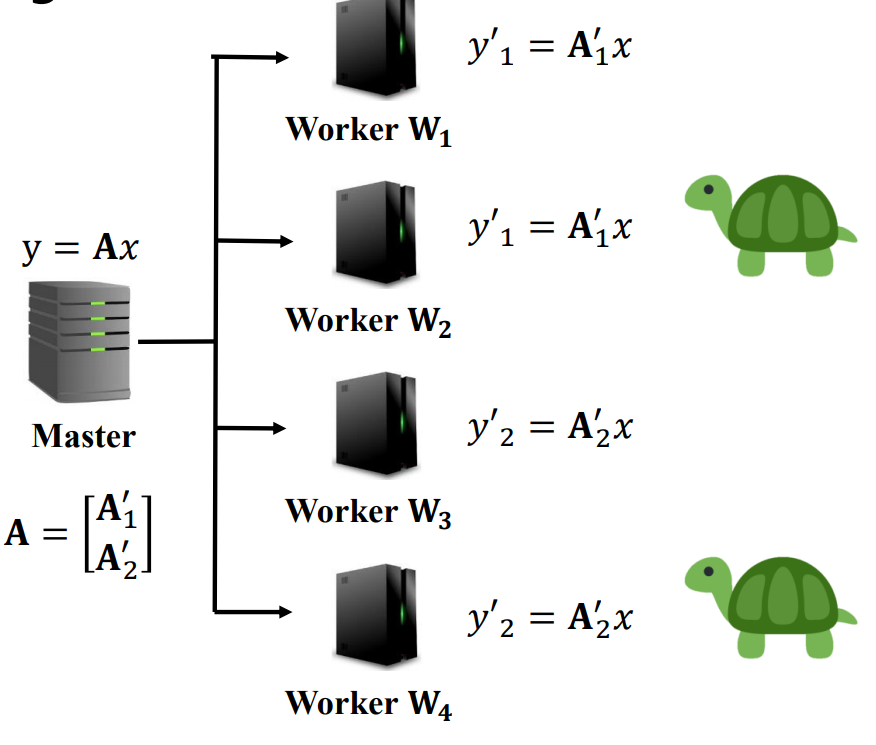
이를 보완하는 방법으로 행렬을 2개 단위로 쪼가서 A1'=[A1,A2], A2'=[A3,A4]로 구성하고, 이 작업을 Worker에게 2개씩 중복되게 할당한다고 생각해보자. 그러면 작업 시간은 W1, W3의 시간 중 가장 느린 작업 시간으로 구성되고, Computation load도 1/2이 될 것이다.(2-repetition)
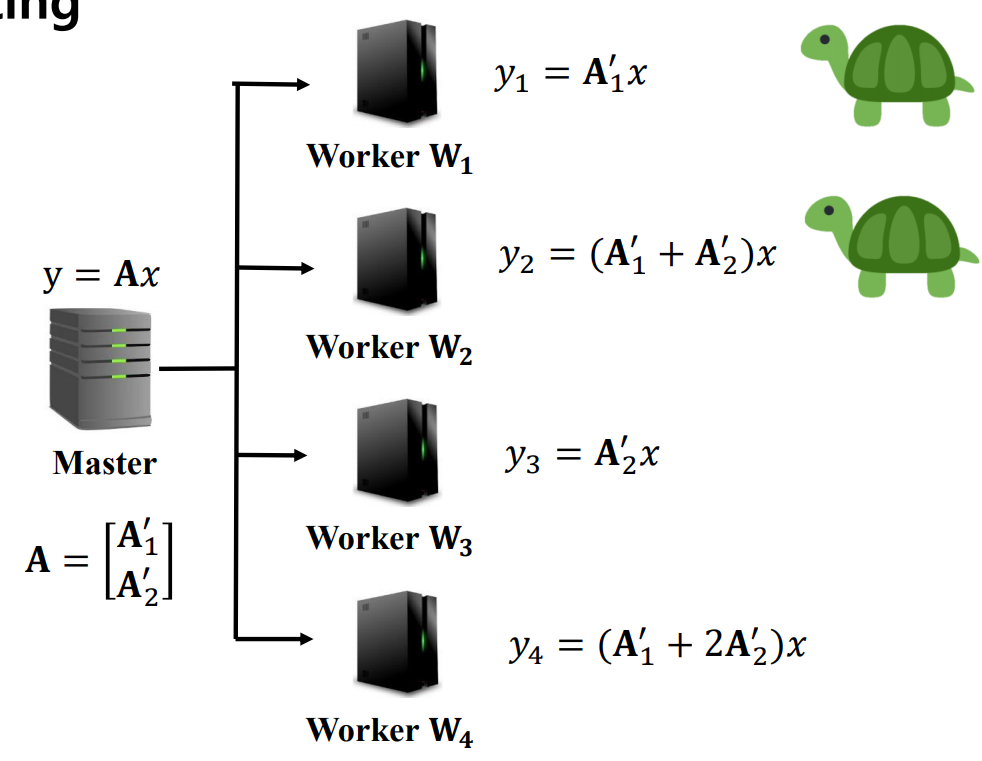
다음은 (n,k) MDS의 방식으로 행렬을 나누어 작업을 중복되게 더해서 배치한다고 생각해보자.
작업 결과는 그냥 받는 Master 쪽에서 수정해서 활용하면 되므로 어디든 2개의 worker의 결과가 오기만 하면 바로 활용하면 된다. 또한 Computation load도 1/2만큼의 부하가 감소된다.
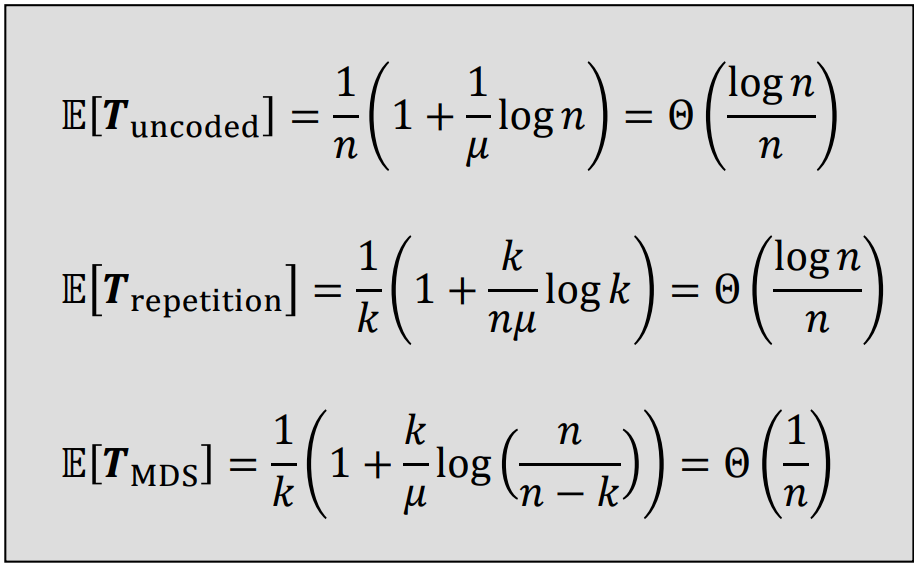
이걸 종합적으로 고려해보면, 위의 사진과 같은 평균 복잡도를 가지게 된다. 즉, MDS 코딩 방식이 Straggler 효과를 최소화 하며 실행시간을 줄이는데 가장 효율적이다.
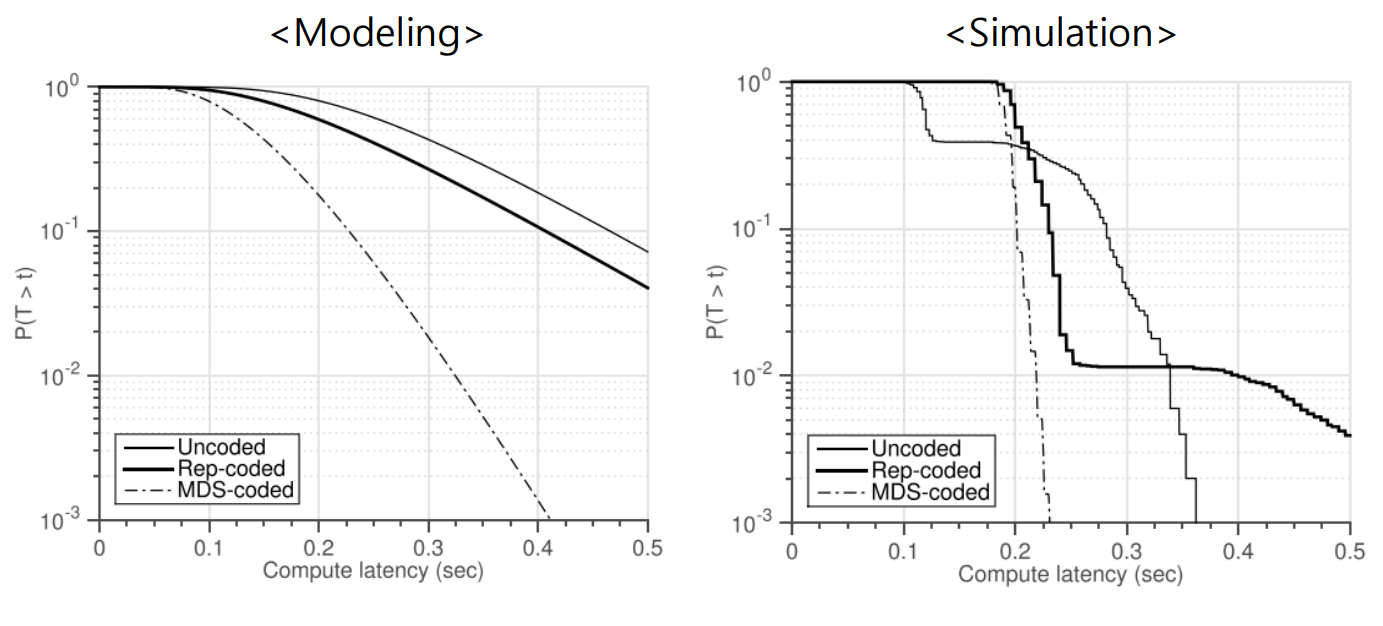
이론상으로는 Uncoded 방식이 compute latency를 늘려도 작업 지연이 가장 많아야하고, Rep, MDS 순으로 떨어져야한다. 그러나 실제 시뮬레이션에서는 MDS는 동일하나 Rep, Uncoded 간에 지연시간이 0.3~0.4 부근에서 역전하는데, 이는 복제에서 발생하는 overhead 때문이다. MDS가 최고의 성능을 보이나, Master server 쪽에서 이를 추가로 처리해야하는 복잡성 증가는 해결해야할 문제이다.
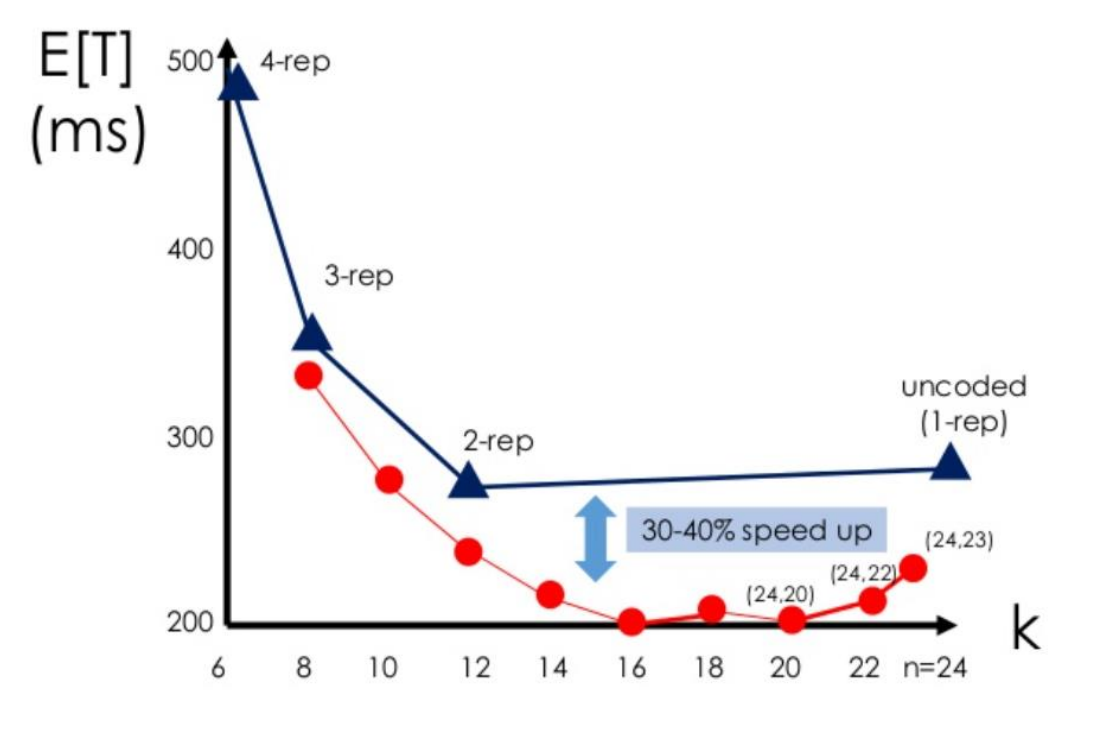
24개의 worker(n=24)를 가정하고, (n,k) MDS code 방법을 사용한다고 해보자.
이 때 n과 k의 관계를 보면, k가 늘어날 수록 작업의 실행시간 기대값은 내려가는 형태를 띄나, 특정 구간 이후로는 다시 상승하는 형태를 보인다. 그 이유는 k가 커지면 작업을 완료하기 위해 결과를 받아야하는 노드 수가 증가한다. 따라서 Straggler의 결과가 필요할 가능성이 늘어나며, 이 때문에 성능이 떨어지는 것이다. k=16 까지는 각 노드가 전체 작업에 처리해야하는 비율이 줄어드는 영향이 더 크다고 볼 수 있다. (M/k)
* Redundancy in distributed computing for matrix multiplication
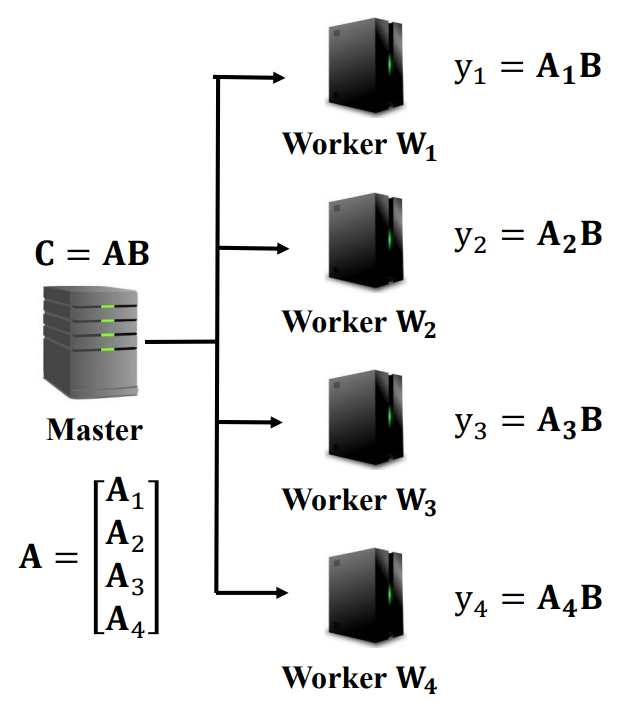
이번에는 행렬곱에서 B가 scalar가 아니라 같은 vector라고 해보자. 기존의 방식대로 A만 분할해서 B와 곱하는 방식은 B의 크기가 커질 때 효율적이지 못하게 될 것이다.
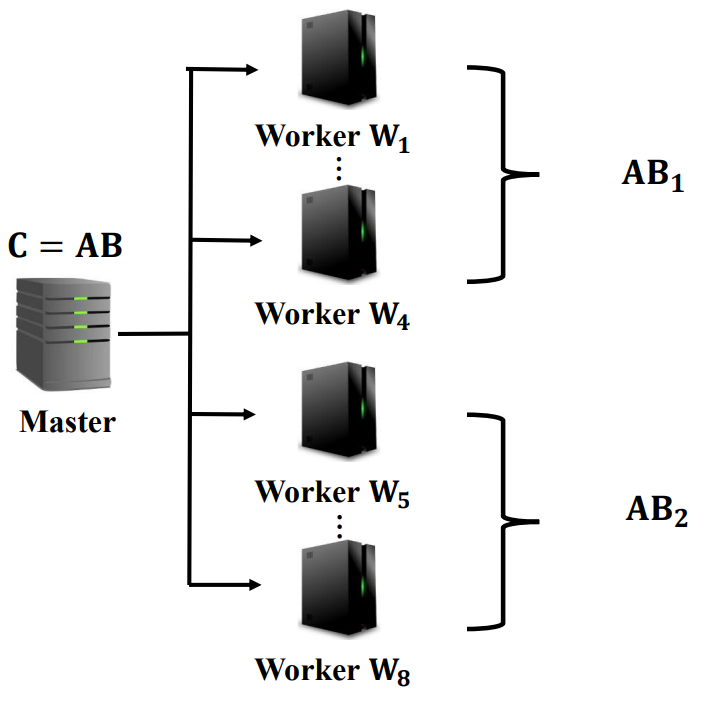
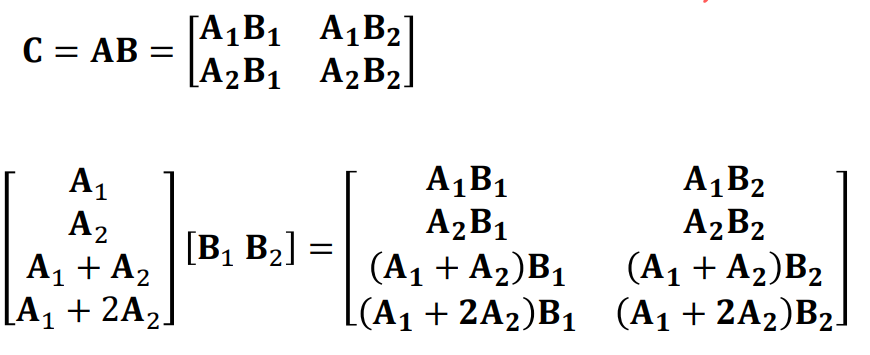
이 때 B까지 분할하고, 분할한 B와 A에 대해 MDS 방식으로 redundancy를 준다고 해보자. 이를 통해 Straggler 영향의 완화와 각 Worker들에게 걸리는 부담도 1/2로 완화가 가능하다.
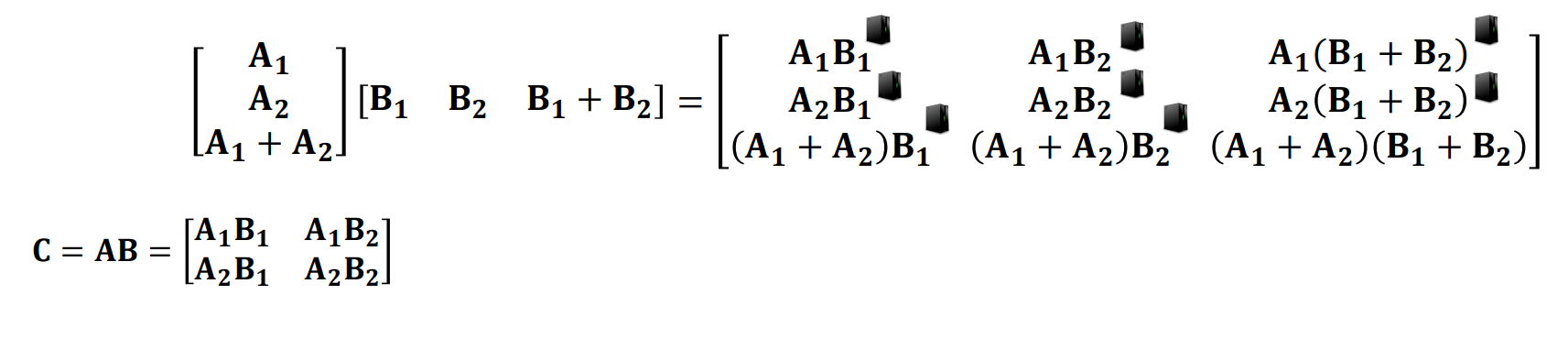
또한 각 행렬의 크기를 고려하여 다양하게 Redundancy를 주는 방법도 적용 가능하다.
위의 사진의 경우는 1행 1열, 1행 2열의 합이 1행 3열인 구조로써 해당 열 중 2개만 존재한다면 나머지 하나를 복원할 수 있는 구조이다. 즉 (9,4) 케이스인 것이다.
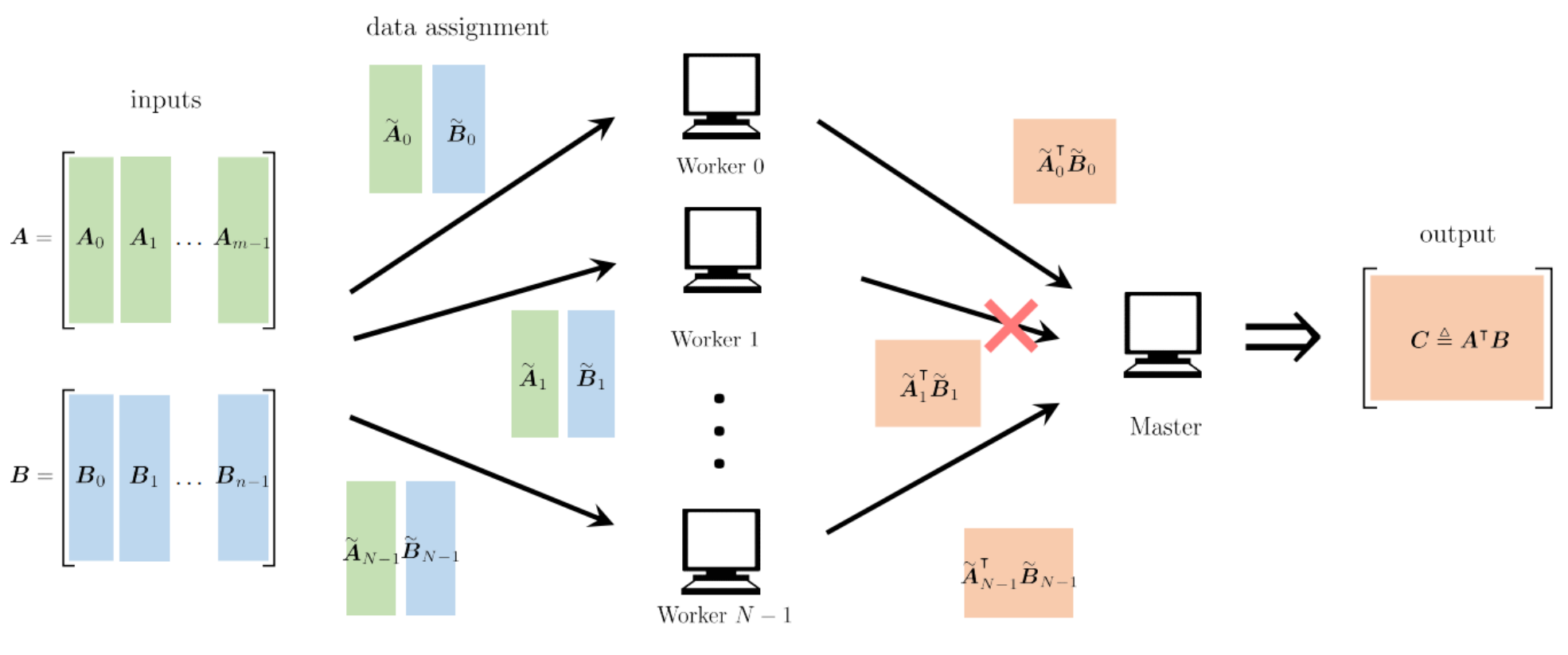
이런식으로 행렬에서 열 단위로 데이터를 쪼게 선형적으로 계산을 분할하는 것을 Polynomial codes라고 한다.
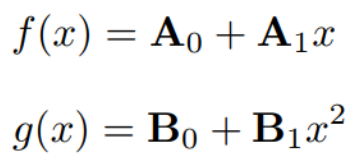
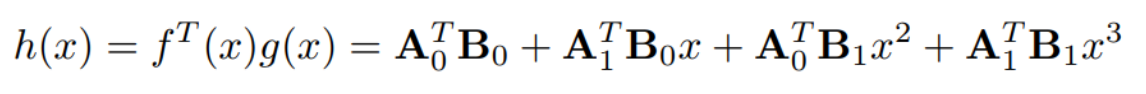
이 케이스를 생각해보자. A=[A0, A1], B=[B0, B1] 이고, 따라서 k=4이다. 4개의 서버만 성공하면 최종 결과를 내는데 문제가 생기지 않는 것이다.
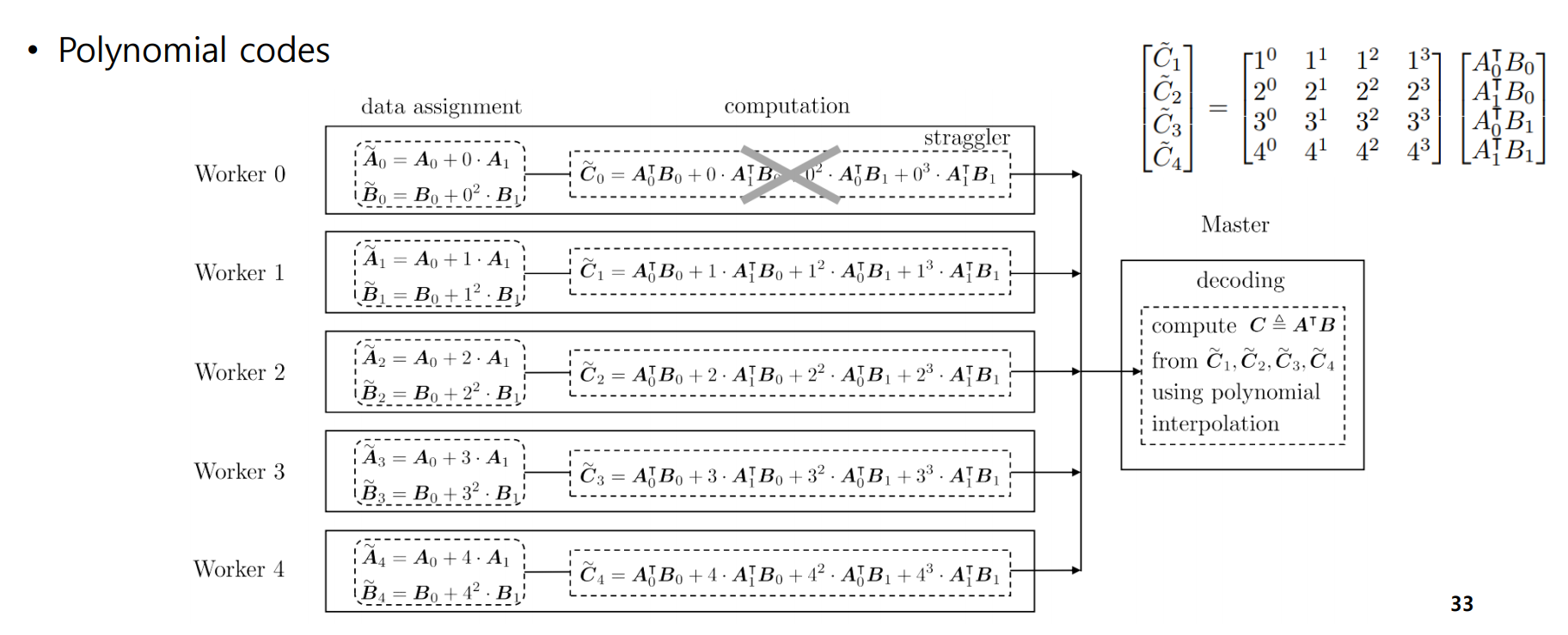
이 때, 이런식으로 data assignment를 A0 + i*A1, B0 + i*B1로 Worker에게 할당해준다고 하자. (Polynomial encoding)
그럼 그 결과는 좌측 위의 행렬과 같은 결과가 나올 것이다. 이때 만약에 Worker 0이 실패한다고 하더라도 C1~C4를 이용하여 복구가 가능한 것이다. 이 경우 (5,4) MDS code 와 동일하다.
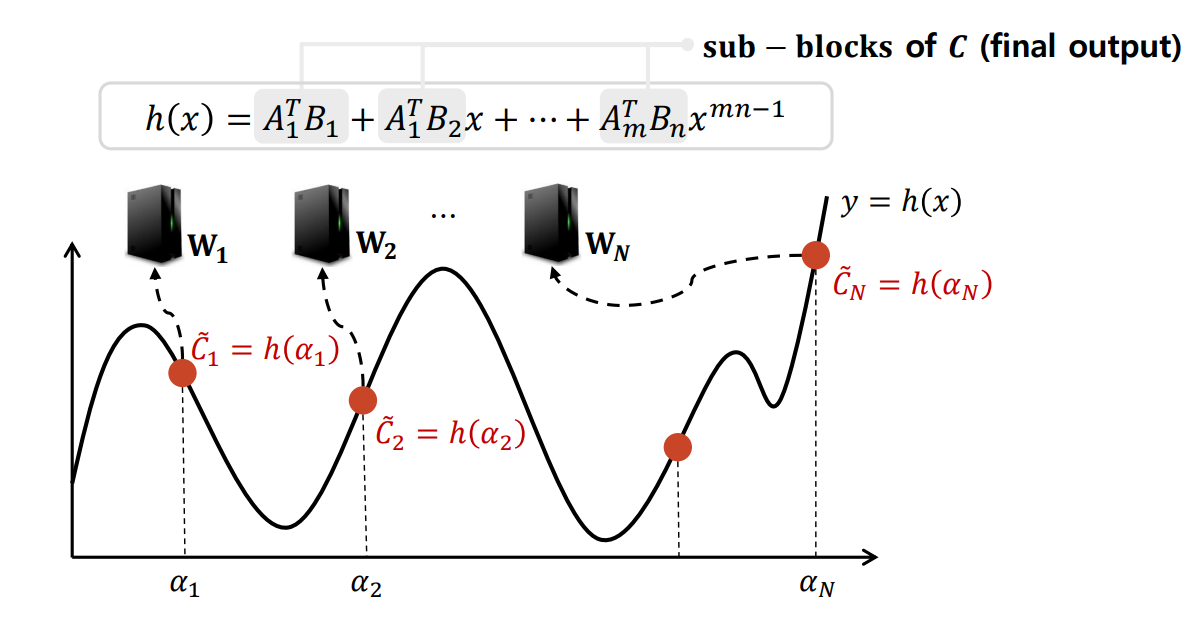
더 구체적인 구현으로 보면, 각 worker node의 계산 결과 값은 h(x)가 될 것이고, 각 서브 블록의 값은 특정 점에서의 평가 값 αi 로 계산된다. 이렇게 구한 h(x)의 특정 점들에서 Lagrange Polynomial Interpolation을 통해 원본 다항식을 복원할 수 있다. 이와 같은 표현을 수식으로 정리하면 다음과 같다.

1. 행렬을 부분 행렬로 나눈다.
2. 각 worker는 부분 행렬로 나뉜 A,B의 polynomial code 들의 곱을 구한다.
3. 이 결과는 mn-1 차수의 polynomial로 표현이 가능하다. (a,b를 1,m으로 설정)
=> 행렬 AB 의 곱을 계산하기 위해 N개의 Worker가 사용된다고 하면, 각 Worker는 A의 1/m 블록과 B의 1/n 블록을 저장하고 계산에 참여한다. 이 경우, Master가 계산을 완료하기 위해 기다려야하는 Worker수는 mn 이다.
'개인 공부' 카테고리의 다른 글
| Distributed System - 10. Distributed Learning Algorithms (0) | 2024.12.06 |
|---|---|
| Distributed System - 9. Distributed Training (0) | 2024.12.05 |
| Distributed System - 7. Consistency & Replication (0) | 2024.12.02 |
| Distributed System - 6. Coordination (0) | 2024.12.02 |
| Distributed System - 5. Naming (0) | 2024.10.23 |